Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic

Session 9

Structural Timber Components Reliability Assessment with Considering Reduction of Structural Timber Strength in Time

Ing. Antonín Lokaj, Ph.D.

VŠB-TU Ostrava, 708 33 Ostrava-Poruba, Czech Republic

antonin.lokaj@vsb.cz

Abstrakt

There is a different approach in verification in ultimate limit states in SBRA method. This alternative approach is based on the simulation technique, load effect combination analysis, the Madison curves, the reduction of structural timber strength in time due to load effects.

Key Words: Timber Structures, Strength Decreasing, Weathering, Reliability Assessment.

1 Introduction

SBRA method (Simulation-based Reliability Assessment method) is documented in textbooks (Marek et al. (1995, 1998, 2001)) containing numerous examples of application related to the assessment of carrying capacity and serviceability. In SBRA method all input values are expressed by variables represented by bounded histograms, the loading is expressed by load duration curves, the reliability function RF = (R – S) is analysed using direct Monte Carlo method and the reliability is expressed by comparing the calculated probability of failure P_f and the target probability P_d given in standards (see, for example, CSN 73 1401-1998 and Table 1).

Tab. 1 Target probability P_d according CSN 73 1401/1998

2 Material Properties

Structural timber is a building material of natural origin. It can be characterized by many positive features: high strenght in relation to its weight, easy processing with machines and tools, nice appearance of timber structures. On the other hand, timber is not a perfect structural material due to its natural origin. It is characterized by negative properties such as: capacity to absorb liquids and vapours from the environment, anisotropy of mechanical properties, anisotropy of swelling/drying processes, inhomogenity of physical and mechanical properties due to occurrence of many natural defects, dependence of physical and mechanical properties on time and environment. Increasing of moisture and durability of load combination effect  in time leads to the reduction of strength of timber. This dependence is nonlinear. This effect on strength of timber was published (f.e.) in Wood (1951).

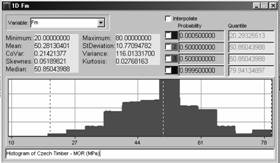
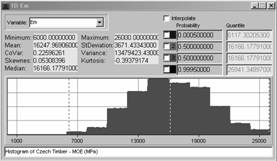
Material properties are expressed by bounded histograms obtained from laboratory tests of timber. For example MOR (Modulus of Rupture) and MOE (Modulus of Elasticity) of Czech softwood –  see Fig. 1.

Fig. 1 Histograms of  MOR (left) and MOE (right) of Czech structural timber [MPa] according: Kuklík P.  and Kuklíková A. (2000)

Duration of load combination effect and moisture content can be expressed by “Madison” – curve (= M-curve) – see Fig. 2 and Eq. (1) and (2).

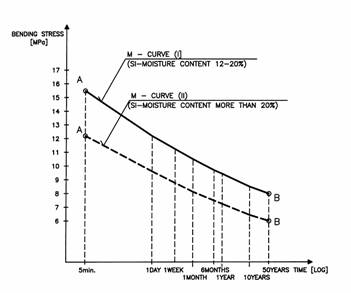
Fig. 2 Example of M-curve for structural  timber (Strength Class SI) and various moisture contents

f_t = f₀ ´ a ´ t ^b                                                                                                          (1)

f_t = f₀ ´ 0,9313 ´ t ^–0,0361                                                                                          (2)

for:       t = 1   [Hour]

where f_t is the time dependent strength of timber, f₀ is the bending strength obtained in standard laboratory test, a and b are coefficients, t is the time in suitable units (1 Hour).

4 SBRA Concept in Timber Element Safety Assessment

The safety assessment in SBRA method is based on load effect combination analysis, the reduction of strength according Madison curves, the analysis of the Safety function and the simulation technique. Fig. 3 express the main ideas of this approach.

A procedure of load effect combination analysis leads to the resulting load effect combination histogram S. Histograms R representes carying capacity of timber element, which is reduced during the time according M-curve (e.g. Madison curve) due to load effect combination. The analysis of the Safety function (SF):

SF = R - S                                                                                                                (3)

in several period during the life span of timber element leads to different values of probability of failures (P_f). We can determine the time, when the probability of failure (P_f) overruns suitable limit for the target probability of failure (P_d) given in specifications (see Tab.1).

Number of simulation steps depends on degree of accuracy, which is required. For common situation seems to be enough 5 mil. simulation steps.

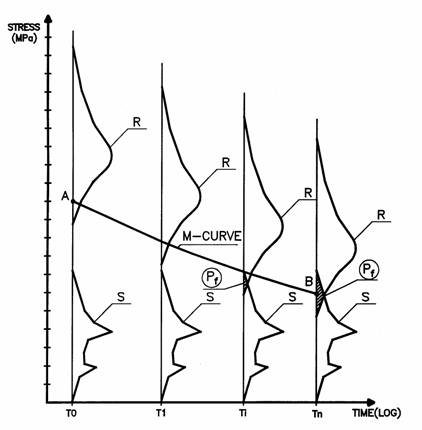
Fig. 3 The safety assessment of structural timber elements based on considering of the reduction of timber strength in time – scheme

5 Example of a tension element exposed to the natural weathering

5.1 Assignment

Assessment of timber tension element carying capacity during 50 years. The timber element with pinned ends and circular cross-section (see Fig. 4) is exposed to an axial force P resulting from combination of  dead, long lasting and snow loads and to the natural weathering.

5.2 Inputs and variables

Diameter of the circular cross-section: d₀ = 100 mm

The extreme load values:

P_dl = 15 kN (Dead load)

P_ll = 15 kN (Long lasting load)

P_sn = 15 kN (Snow load)

P = P_dl ´ P_dl,var + P_ll ´ P_ll,var + P_sn ´ P_sn,var                                                                              (4)

Histograms: P_dl,var , P_ll,var , P_sn,var representes variability of the loads.

Material: Czech structural timber – according: Kuklík and Kuklíková (2000), histograms – see Fig. 1.

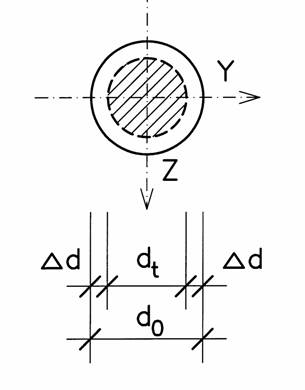
Fig. 4  The tension timber element cross-section exposed to the natural weathering

Relation between tension and bending stregth (according CSN EN 338):

f_t,0,k = 0,6 f_m,k                                                                                                                         (5)

The rate of cross-section erosion (decreasing) due to the natural weathering of structural timber (according Williams et al. (2001)) is supposed 9,0 mm/100 years. That means:

Dx = 1,027´10^-8          [m/Hour]                                                                                              (6)

A time dependent area of the cross section:

A_T = p ´ d_T² / 4 =  p ´ (d₀ – 2 ´ T ´ Dx)² / 4                                                                                  (7)

5.3 Safety assessment

Safety assessment was made by analyzing the Safety function (SF=R-S) in selected time sections for 5 mil. simulation steps.

Time dependent carying capacity R:

R = 0,9 ´ 0,6 ´ F_m ´ 0,9313 ^(-0,0361)                                                                                      (8)

Time dependent effects of load combination S:

S = P / A_T                                                                                                                             (9)

During the time the carying capacity of the timber element (R) falls due to reduction of timber strength and effects of load combinations (S) increases owing to decreasing of effective area of the cross section exposed to natural weathering. These facts evoke the increasing of the calculated probability of failure in time. Results – see Tab. 2.

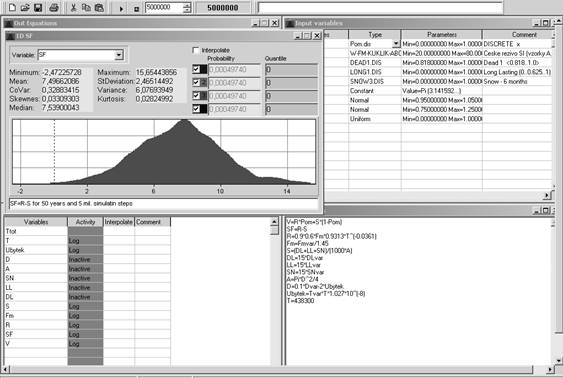
Fig. 5 The Safety Function (SF = R-S) - probability of failure P_f = 0,0004974 after 50 years (5 mil. simulation steps). Output of AntHillä computer program

5.4 Results

Tab. 2 containes values of probability of failures of the structural timber element in selected time sections.

Tab. 2: The probability of failures (P_f) in selected time sections 

It appears, that timber element will be satisfied for high level of importance only for 1 year, for common level of importance for 20 years and for low level of importance for 50 years.

6 Conclusions

SBRA method introduces qualitatively new approach in the structural design corresponding to the computer era. It allows the designer for better understanding the actual safety and serviceability of timber components. The application of Monte Carlo simulations technique corresponds to the potential of computers available to all designers.

Acknowledgments

This work has been supported by the Grant Agency of Czech Republic grant No. 103/01/1410 "Application of the new generation of probabilistic methods in the assessmentof structural safety, serviceability and durability".

Special thanks to Assoc. Prof. P. Kuklík, Ph.D. for affording the statistical data of czech structural timber strength.

References

[1] Marek, P., Guatar, M. and Anagnos, T. (1995) Simulation-based Reliability Assessment for Structural Engineers, CRC Press, Inc., Boca Raton, Florida.

[2] Marek, P., Guatar and Bathon, L. (1998) Tragwerksbemessung. Von deterministischen zu probabilistischen Verfahren,  ACADEMIA Praha.

[3] Marek P., Brozzetti J. and Guatar M., (editors), (2001) Probabilistic Assessment of Structures using Monte Carlo Simulation – Backround, Excercises and Software, ITAM CAS Praha.

[4] Marek, P., Guatar, M., (1988-2001), Computer programs DamAc™, M-Star™ , AntHill™ (Copyright), Distr. ARTech, Nad Vinicí 7, 143 00 Praha 4.

[5] Wood L.W. (1951) Relation of stregth of wood to duration of load, U.S. Forest Products Laboratory Report No. 1916.

[6] Kuklík P., Kuklíková A., (2000) Metody zjiatování vlastností dreva na stavební konstrukce, Stavební obzor 8/2000, str. 242-245, Praha.

[7] Kuklík P., Doleja J. (1998) Nondestructive Evaluation of Structural Timber. Proc. 5th World Conference on Timber Engineering, Montreux, pp. 692-699.

[8] Kuklík P., Kuklíková A. (2000) Nondestructive Testing of Solid Timber. Proc. International Conference on Wood Fiber Composites, Stuttgart, pp. 303-312.

[9] Williams R. S., Knaebe M. T.,  and Feist W. C., (2001), Erosion rates of wood during natural weathering. Part II. Earlywood and latewood erosion rates. Wood and Fiber Science, 33 (1), p. 43-49.

[10] CSN EN 338, (1996), Konstrukcní drevo – Trídy pevnosti, Praha, CNI.