Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic

Session 9

Optimization Study of Beam with Sudden Profile Change

Jan Hlaváček

Jankovcova 32, 17000 Prague, Czech Republic

jan.hlavacek@mybox.cz, http://hlavacek.mainpage.net/

This paper deals with the application of the SBRA (Simulation Based Reliability Assessment method [1]) for safety assessment of a welded steel beam with a sudden profile variation. Close attention is paid especially to the determination of the position where the profile changes.

Assignment

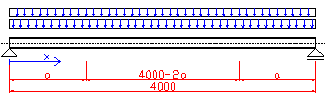
The beam is simply supported. The span is L = 4 m, the material grade is steel S235. The beam is exposed to two uniformly distributed loads. The design values are: dead load g = 10 kN/m, long lasting live load q = 8 kN/m. Assess I-profiles of this steel welded beam (see Fig. 2) regarding the bending moment. Determine the position where the profile is to be changed with respect to material savings. Lateral-torsion buckling of the beam is prevented. Do not assess the serviceability limit state. The design probability of failure is P_f,lim £ 0.00007.

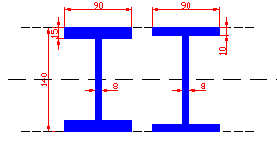
Fig. 1 Beam scheme                                      Fig. 2 Profile 1,          Profile 2

Structure Response to the Load 'S'

The variable value of the load is equal to the product of its maximum value and the coefficient expressing its variation by the assumptive distribution, then g = 10 kN/m ∙ g_var,
q = 8 kN/m ∙ q_var. Individual distributions follow in the chart (Fig. 3).

 Fig. 3 Variables of the response

The bending moment behavior along the beam M_x = ½ ∙ (g + q) ∙ (L ∙ x - x²) is traced by the AntHill [1] software. The variables taking part in this simulation are g, q.

Fig. 4 Structure response, dispersion of the bending moment M_x along the beam

Structure Resistance 'R'

The variable value of the steel yield stress is equal to the coefficient expressing its variation by the assumptive distribution, then f = f_var. The variable values of the profile moduluses are equal to the products of their nominal values and the coefficients expressing their variation by the assumptive distributions, then W₁ = W_1,nom ∙ W_var, W₂ = W_2,nom ∙ W_var. Individual distributions follow in the chart (Fig. 5).

Fig.5 Variables of the resistance

The nominal values of the cross-sections properties are W_1,nom = 1.64E^-4 m³, W_2,nom = 1.25E^-4 m³. The profiles 1 and 2 are displayed on Fig. 2.

The structure resistance is defined as the product M_r = W ∙ f, than M_r1 = W₁ ∙ f, M_r2 = W₂ ∙ f.

Assessment

Critical cross-sections, considering the bending moment, are for Profile 1 the center of the beam (x = 2 m), for Profile 2 the place of its sudden profile variation (x = ?).

Profile 1, x = 2 m

In the center of the beam's span is the failure probability P_f = 0.000053 < P_f,lim = 0.00007. Profile 1 satisfies the requirements, calculated by the AntHill [1] software.

Fig.6 SFF1, cross-section of Fig.7 in the span center (x =2 m), P_f is determined by the intersection of the resistance and response graphs

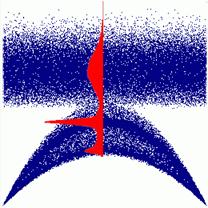
Fig. 7 AntHill: response M_x and resistance M_R1

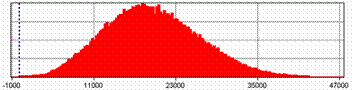
Fig. 8 SF1 = R – S

Profile 2, x = ? m

With assistance of the AntHill [2] software, the probability of failures is found in individual positions near the estimated location of the sudden profile change.

Fig. 9 Optimization, probability of failure calculating P_f near the sudden change location

The profile should be changed in position x = 1 m from the support. The failure probability in this location P_f = 0.000027 (see Fig.9) < P_f,lim = 0.00007. Profile 2 satisfies the requirements. Calculated by the AntHill [2] software. 

Fig. 10 SFF2, cross-section of Fig.11 in the x =1 m position, P_f has been determined by the intersection of the graphs of resistance and response

Fig. 11 AntHill: response M_x and resistance M_R2

Fig. 12 SF2 = R – S

Global Analysis of Profile 1 and 2

MS(x)

MR2

Fig. 13 Response and resistance, bending moments M_x, M_R1, M_R2  

Additional Study

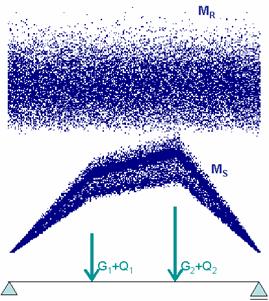
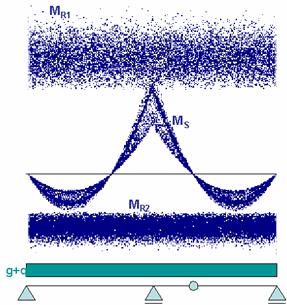
Fig. 14 AntHill: response M_s and resistance M_R

Conclusions

This study outlines the opportunity of using the SBRA method [1] for the global reliability assessment. The used example is very simple; however, it is possible to asses more complicated statically determined structures.

Literature

[1] Marek P., Gustar M., and Anagnos T. (1995). Simulation based reliability assessment for structural engineers. CRC Press, Inc, Boca Raton, Florida.

[2] Probabilistic Assessment of Structures using Monte Carlo Simulation; editors: P. Marek. J. Brozzetti, M. Gustar; publisher: ITAM CAS CR, Prague 2001.