Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic

Session 8

Safety Assessment of a Frame

Ing. Petr Konečný

Pustkovecká 48, 70800, Ostrava - Pustkovec, Czech Republic

petr.konec@volny.cz

1.      Introduction

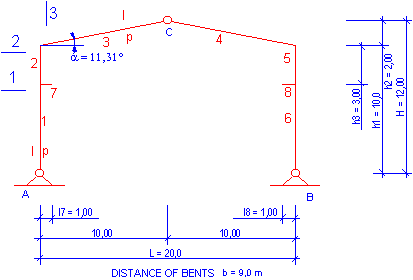
The subject of this study is the safety assessment of members of the steel frame (see Fig. 1) by fully probabilistic SBRA method [3]. Study outline possibilities of the SBRA in the assessment of systems with multi component load effects combination. Assessment by the SBRA is compared with another one performed in accordance with the European ČSN P ENV 1993-1 [2] (shortly denominated as EC).

There are differences between both methods:

(a)    EC [2], which uses load and resistance factors, looks more likely deterministic and reference value of safety is defined by plastic carrying capacity of the shape. The safety assessment according to EC is published in [4].

(b)    SBRA [3] characterize random variables (e.g. loading) by their extreme and  bounded histograms. The maximum (extreme) load effects according to SBRA [3] correspond to the factored load effects according to EC. Carrying capacity of the shape is defined by onset of yielding. Safety of the structure is expressed by probability of failure P_f < P_d. Next part of the paper describe assessment using SBRA method.

2.      Assignment

Statically determinate plane steel frame (see Fig. 1) is a part of bent of industrial building. Loadings considered in this study are wind, snow, crane girder and dead load (Fig. 2). The second order effects, the buckling and torsion-buckling, are not considered in this study. Safety of the selected cross sections (see Fig. 1) is assessed. The effect of shear forces is neglected.

Fig. 1. Geometric chart of the frame

 3.      Geometrical and material properties

Proportion and lengths are considered as deterministic. Variation of cross-section area is characterized by appropriate histogram.

4.      Loadings

Planar frame is exposed to dead load, wind load, snow load and crane girder (vertical and horizontal forces) (see Fig. 2). Loadings are considered mutually statistically uncorrelated. Extreme load effects correspond to the factored load effects according to EC (National aplication document of [1])

Fig. 2. Loadings

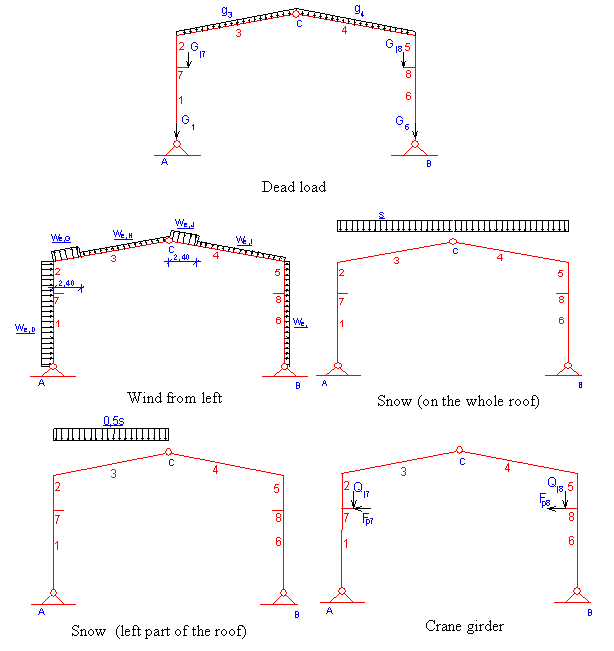
SBRA allow to anylize wind or crane girder forces to act from the left side or the right side. Direction of forces depend on each simulation and is characterized by appropriate histogram.

5.      Internal forces and load effects combination

Transformation model analyze inner forces of the frame (Axial forces and Bending moment). Model allow to investigate inner forces in the critical cross-sections (see Fig. 1) and allow to create inner forces scatter (see Fig. 4).

The single component load effects combination S_SBRA (see /1/) investigate axial forces N_i [kN] or bending moment M_i [kNm] using bounded histograms (represented by G_VAR and Q_VAR) and extreme value of each specific loading.

                                                                  /1/

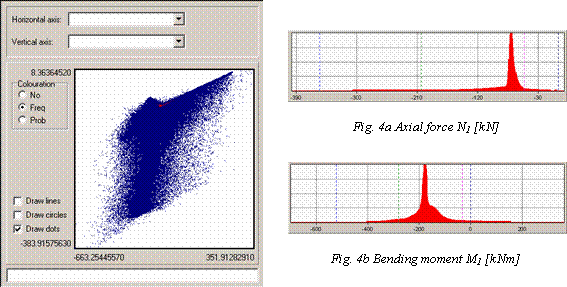
Fig. 3. Two component load effects combination (M_i - horizontal axis, N_i – vertical axi)s

Fig. 4. Scatter of bending moments M [kNm] (left) and axial forces N [kN]

SBRA method [3] allows making multicomponent load effects combination. Formula /2/ investigate stress s_i [kPa] in the critical cross-sections, where A_i [m²] is area, W_el,y,i [m³] is section modulus. Variables with subscript var are represented by appropriate histogram (see Table 1). Load effects combination, expressed by stress s_i, for axial forces N_i and bending moment M_i is done in one simulation step (see Fig. 3).

                        [kPa]                                                             /2/

6.      Reliability assessment

Reliabilty assessment by SBRA method is based on the limit state philosofy. Stochastic character of variables is represented by histograms.

SBRA analyze safety function SF_i [kPa]  /4/, where R_SBRa,i /3/ [kPa] is resistence (defined by onset of yielding) and s_i [kPa] /2/ is stress due to load effect combination.

 R_SBRA,i = f_y,i /g_M = f_y,i/ 1.15     [kPa]                                                                                    /3/

 SF_i = R_SBRA,i - ABS (s_i)          [kPa]                                                                                    /4/

Probability of failure P_f,i /5/ is function of safety function SF_i [kPa] /4/ in the investigated fibre.

P_f = P(R_SBRA,i - S_SBRA,i<0) =P(SF<0)      […]                                                                /5/

Safety condition P_f < P_d comply for all cross-sections

7.      Conclusion

Assessment of the planar frame according to EC [2] has 144 cases of the load effects combinations. Combination of the load effects for a three-dimensional frame could has many more load effects combinations.

Study denotes possibilities of the SBRA [3] in analyzing of the multi component load effects combination and determining of the steel frame reliability.

In this example are shapes designed according to EC [1], [2] more conservative than designs according to SBRA providing considered conditions (see Table 4).

References

[1] ČSN P ENV 1991-1, Basis of design and actions on structures, Part 1: Basis of design Eurocode 1, ČNI, Prague, 1994.

[2] ČSN P ENV 1993-1-1, Design of steel structures, Part 1-1: General rules and rules for building, Eurocode 3, ČNI, Prague, 1994.

[3] Marek, P., Brozetti, J., GUŠTAR, M. (editors), Probabilistic Assessment of Structures using Monte Carlo Simulation, ITAM CAS, Prague, 2001.

[4] Konečný, P., Master thesis: Posudek spolehlivosti vybraných konstrukčních dílců podle norem eurocode a metodou SBRA, FAST VŠB-TUO. Ostrava 2002.