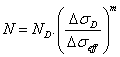
Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic
Session 6
Fatigue-Reliability Assessment of Steel Structures
Doc. Ing. Miloš Vlk, CSc.
Dept. of Mechanical Engineering, Brno University of Technology
Technická 2, 616 69 Brno, Czech Republic
Abstrakt
Reliability methods are applied in design against fatigue and fracture of welded steel structures. Limit states determined by failure criteria are provided based on fatigue damage accumulation using Miner´s rule in connection with S-N curves and fatigue crack growth using fracture mechanics.
Key Words: fracture mechanics, life prediction, reliability assessment, subcritical crack growth
Fatigue fracture of engineering structures has been recognized as an important cause of their failure. However, fatigue is a very complicated process that is difficult for accurate description and prediction.
Available informations indicate that most fatigue failures result from poor design. For welded structures, defects are generally present as small cracks or crack-like defects initiated at the time of fabrication. Final fracture is then a combination of crack growth and overload failure.
Current design procedures are essentially deterministic, which, however, results in wide discrepancies in design safety levels due to different uncertainties in applied models, material parameters, random loads and load effects, etc. To achieve consistent safety levels, probabilistic treatment of these random quantities is therefore the most appropriate.
The theory and methods of structural reliability have been developed – see e.g. [1]. When considering multi-random variable input resulting from statistical and probabilistic evaluation of data, analysis of reliability based on analytical mathematical solutions can become extremely difficult or even impossible. An alternative approach, which has become very efficient due to modern computer technology, is to use the methods based on simulations. Monte Carlo simulation (direct simulation) technique is a very a powerful and convenient tool for evaluation the probability of failure of structural components ( [2], [3], [4] ). The computational effort per simulation cycle is relatively small, the number of simulation cycles is relatively high – especially for low probability of failure. The system failure probability should be calculated according to the actual failure probability of the components and their correlations.
The steel structure is usually subjected to repeated loadings and is exposed to environmental effects as it ages. Thus, steel as a material degrades with time and cracks, even in a very minute form, are expected to grow with time. Accumulated-fatigue damage leading to eventual fracture is one of the major concerns in deciding whether the life of a steel structure can be safety extended.
The physical process of fatigue can be divided into three phases (see e.g. [5] ):
· the crack-initiation phase,
· the subcritical crack-propagation phase (this is the most important period in the engineering fatigue-resistance design, since it takes about 95 % of the total fatigue life in many cases); flaws are inherent in many components owing to the process by which they are manufactured or fabricated,
· and the fracture stage.
The experimental and theoretical studies were conducted to understand each of these phases as accurately as possible. All these studies can be classified into two groups :
1. the studies based on experimental data, which led to the development of the S-N curves (nominal stress, structural stress and notch stress approaches),
2. the studies based on crack-propagation theory (fracture mechanics approach).
An S-N curve is given as
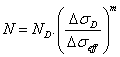
where N is the number of cycles to failure (total fatigue life) under constant-amplitude stress range, ND , DsD, m are S-N parameters, Dseff is effective stress range (with respect to two slopes of S-N curve and its cut-off level below which no damage is accumulated).
The fatigue damage accumulation Db (due to application of the block with different stress levels Dseff,i , i = 1 .... s, each with number of cycles ni) follows Miner´s law as
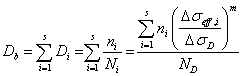
Number of blocks to reach the limit damage for failure DM is then
![]()
It can be concluded, that the uncertanties and scatter in the
· load process (load spectra),
· geometry effects,
· material properties and fabrication (chemical composition, hardness, metallurgical homogenity, welding process, welding treatment),
· environment (corrosion atmosphere, temperature, humidity, irradiation),
are significant ([6], [7], [8]). They must be considered in any comprehensive fatigue-evaluation procedure.
Variability of the load process and geometry effects implicates the wide band stress proces. For identification the number of cycles and their stress ranges is the rainflow method the most accurate model. For a long term measurement under representative operational conditions the suitable portable analyzers are now supplied. Statistical analysis of the results obtained leads to a proper type of distributions for Dseff,i and ni and their parameters.
Statistical analysis of the fatigue data (reflecting material properties, fabrication and environment) in simple approach leads to a ND as random variable and exponent m and endurance limit DsD as a constants. Lognormal distribution of ND provides a good fit to cycles-to-failure data.
Complications in the random fatigue problems (the specific history of stress response) are taken in variability of the limit damage for failure DM . For purposes of reliability analysis it is reasonable to model DM as being lognormal.
An example of reliability assessment of welded connection according to the foregoing principles using Monte Carlo simulation technique, a procedure leading to the determination of the service life considering a selected probability of failure, is presented in Fig. 1.
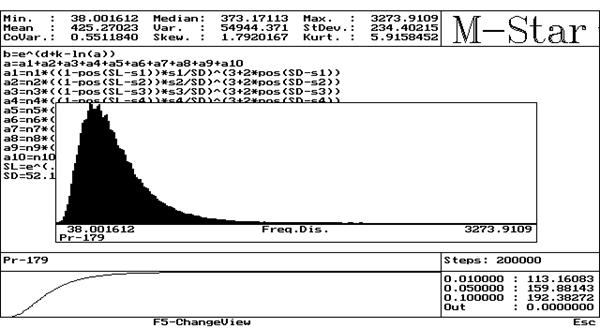
Fig.
1 Distribution of number of blocks to failure
The basic parameter of fracture mechanics fatigue analysis is the stress intensity factor range given by the following relationship [9]
![]()
in which Ds is the applied stress range, a is the crack depth for a surface flaw (or half-width for a penetration flaw), Y is a finite geometry correction factor defined
![]()
in which Mm is correction function dependent on crack size and shape, proximity of the crack tip to free surface and loading; the Ms is correction function dependent on the type, shape and dimensions of the weld connection with crack; the F is complete elliptic integral of the second kind depending on the ratio of the crack depth and length. The functions Mm and Ms are usually obtained by FEM; for many geometries the results are provided in some handbooks and standards (e.g. [10]).
The subcritical crack growth rate is governed by the Paris – Erdogan law
![]()
in which C and m depends on material and environment.
A convenient equation for cycles to failure DN can be derived by integrating from from an initial crack length a0 to a critical length aK (for DK greater then threshold stress intensity factor range):
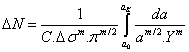
The critical-crack length can be defined as the size of the crack causing the failure or a design-crack size beyond which the serviceability requirements cannot be satisfied.
Let us consider
two possible limit states – brittle fracture (crack growth
becomes unstable when the crack length is aC) and
plastic collapse (deformations become unbounded due to stable crack
growth – limit crack length is aL). Thus the
critical length aK is
![]() .
(Next possibility is to consider the serviceability requirements –
e.g. for pipelines and pressure vessels leakage of liquid or gas.)
.
(Next possibility is to consider the serviceability requirements –
e.g. for pipelines and pressure vessels leakage of liquid or gas.)
To reflect fatigue under variable-amplitude stresses, the cycle-by-cycle method is usually used.
Condition for brittle fracture is
![]()
in which KJC is the fracture toughness. According to the „master curve“ [11] is
![]()
whereas T is the operational temperature, T0 is the temperature at which the mean fracture toughness is 100 MPa.m1/2.
Limit crack length aL for plastic collaps can be assumed e.g. according to [12].
An advantage of applying the fracture mechanics approach is that reliability can be easily updated upon additional inspection and repair results (see e.g. [4], [7], [13].).
For fracture mechanics analysis purposes is assumed ([14]):
· The cracks are generally idealized as elliptical or semi-elliptical.
· Initial-crack size (the crack size from which the fatigue crack will propagate):it is the lower limit of the crack size that can be first detected reliably by a specific type of equipment. The distributions most frequently suggested in modeling the uncertainty in the initial-crack size are the lognormal and the Weibull distributions.
· Crack aspect ratio (ratio of the length along the minor axis to the length along the major axis). This is a very important parameter in estimating the geometric function for determination of stress intensity factor. Usually is considered to be lognormally distributed.
· Material properties for subcritical crack growth. For steel the fatigue-growth parameter C approximately follows a lognormal distribution. The fatigue-growth exponent m is assumed to be a constant.
· The fracture toughness is often subjected to considerable scatter (especially for low- and intermediate-strength steels that undergo a ductile-to-brittle transition). The temperature T0 is considered to be normally distributed. The same distribution type is used for operational temperature T.
· Critical crack size is determined based on either the serviceability requirements or fracture criteria (usually brittle or ductile fracture)
The fatigue reliability of welded steel component according to the nominal stress and linear elastic fracture mechanics approaches are evaluated considering several sources of uncertainties. Simulation using Monte Carlo method is a convenient tool for evaluating the probability of failure and is easily adaptable for fatigue problems.
Acknowledgements. This work has been supported by the Grant Agency of Czech Republic grant No. 103/01/1410.
[1] Sundararajan C. (Ed.): Probabilistic Structural Mechanics Handbook – Theory and Industrial Applications. Chapman & Hall, New York 1995.
[2] Marek, P., Guštar, M., Anagnos, T.: Simulation-based Reliability Assessment for Structural Engineers. CRC Press, Inc., Boca Raton, Florida, USA, 1995.
[3] Marek, P., Brozzetti, J., Guštar, M.: Probabilistic Assessment of Structures using Monte Carlo Simulation. ITAM Praha 2001.
[4] Vlk, M.: Application of Simulation Technique in the Assessment of Safety of Structural Components exposed to Fatigue. Progress Report. Project No. 103/94/0562. Grant Agency of Czech Republic 1996.
[5] Radaj, D.: Design and Analysis of Fatigue Resistant Welded Structures. Abington Publishing, Cambridge 1990.
[6] Harris, D.O.: Probabilistic Fracture Mechanics. In: [1]
[7] Sobczyk, K. (ed.): Stochastic Approach to Fatigue – Experiments, Modelling and Reliability Estimation. Springer Verlag, Wien 1993.
[8] Schijve, J.: Fatigue Predictions and Scatter. Fatigue and Fracture of Engineering Materials and Structures, 17 (1994), No. 4, pp. 381-396.
[9] Anderson, T.L.: Fracture Mechanics – Fundamentals and Applications. CRC Press, Boca Raton 1995.
[10] BS 7910:1999 – Guide on Methods for Assessing the Acceptability of Flaws in Fusion Welded Structures.
[11] Wallin, K.: Innovative Approaches to Irradiation Damage and Fracture Analysis. The 1989 ASME Pressure Vessel and Piping Conf., Honolulu, July 1989.
[12] Shen, G., Tyson, W.R.: Ligament-Yield Load of Plates and Cylinders with an Axial Semi-Elliptical Flaw. Fatigue and Fracture of Engineering Materials and Structures, 18 (1995), No. 7/8, pp. 777-787.
[13] Zhao, Z., Haldar, A.: Bridge Fatigue Damage Evaluation and Updating Using Non-Destructive Inspections. Engineering Fracture Mechanics, 53 (1996), No. 5, pp. 775-788.
[14] Wirsching, P.H.: Probabilistic Fatigue Analysis. In: [1]