Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic
Session 4
The role of reference values - Examples
Prof. Ing. Jaroslav Menčík, CSc.
University of Pardubice – Jan Perner Transport Faculty
Studentská 95, CZ 532 10 Pardubice, Czech Republic
Abstrakt
The meaning of reference (limit) values is illustrated on two examples of an elastic-plastic beam loaded by concentrated force. In the first example, the load is static and the limit states are the maximum deflection or rise of plastic deformations. In the second example (impact load), the reference values are the maximum bending moment and residual deflection after unloading. As there is no explicite relationship between the energy of impact and the force in the elastic-plastic state, the Response Surface Method in combination with Monte Carlo technique is used. The choice of reference values and allowable probabilities of their exceeding is discussed.
Keywords: Reliability assessment, failure, limit states, simulation, Monte Carlo Method, Response Surface Method, elastic analysis, plastic deformations, impact.
1 Introduction
Reference values are closely related to limit states. While a limit state characterizes the possible failure of an object in a qualitative way (e.g. plastic collapse), the reference quantity characterizes the resistance of the object in a measurable way (e.g. bending moment), and the reference (or limit) value is such value of the reference quantity, whose exceeding means failure. Because the quantities that have influence on the function and reliability of the component or structure, often have random character; (e.g. load or material characteristics), it is reasonable to use probabilistic methods for the reliability analysis (e.g. SBRA), and consider (and choose) the reference values as those, which may be exceeded with some small probability. The allowable probability should depend on the consequences of exceeding the pertinent value - cf. a small exceeding of the allowable deflection of a beam and a "small exceeding" of strength of a load carrying principal structural part.
The basic terms and concepts of reference values are explained in the monographs [1, 2] by Marek et al., and were also discused in detail at this colloquium [3, 4]. In this paper, the role of reference values will be illustrated on two examples of a simply supported steel beam, loaded by a concentrated force in the middle between the supports. The task is to find the cross-section dimensions of the beam.
2 Example 1 – dead load, common operation
The force is caused by the body hanging on the beam. Two limit states are considered: 1) no plastic deformations may arise in the beam, 2) the maximum deflection under the load must not be larger than some prescribed value. Thus, the first problem is to check whether the maximum bending stress,
s = M / W, (1)
does not exceed the yield strength fy of the beam material. M = FL/4 is the maximum bending moment, L is the span, W is the elastic section modulus, and F is the force related to the mass m of the hanging body by F = gm, where g = 9.81 ms-2 is the acceleration due to gravity. As plastic deformations could arise, and an ideal elastic-plastic material without strain hardening will be assumed (so that the stress cannot exceed fy), the reference quantity will be the maximum bending moment, with limit (reference) value corresponding to the state when the maximum stress in the beam attains the yield strength; RV = My = fyW. Then, the reliability condition (or limit state function) can be written as
RF1 = M / My < 1 , (2)
The second condition for reliability is:
RF2 = d - y > 0 , (3)
where d is the maximum allowable deflection (reference value) and y is the deflection under load F. For elastic deformations,
y = FL3 / (48EJ) ; (4)
E is the elastic modulus and J is the moment of inertia of the cross section. For simplicity, rectangular cross section (width b and height h) is assumed. Then, J = bh3/12 and W = bh2/6.
The mass of the body, as well as the dimensions of the cross section and yield strength of the beam are random variables. Thus, the problem will be analysed using the Monte Carlo technique [1, 2]. Also, some probability of exceeding the reference values will be permitted.
The input variables have the following parameters (distribution, mean, standard deviation): b (normal, 40 mm, 0.3 mm), L (constant, 2000 mm), m (normal, 1500 kg, 150 kg), E (constant, 210 000 Mpa), fy (steel S 235, the histogram used in [5]), with the minimum and maximum values 200 MPa and 395 MPa), d (constant, 5 mm). The quantity to be found is the beam height h, and can be chosen from nominal values 80 - 85 - 90 - 95 - 100 mm. The actual heights have normal distribution, with standard deviation 0.5 mm.
Both limit states are related to serviceability, with no danger of collapse or heavy damage. Thus, higher probabilities of „failure“ are allowed: the yield strength may be exceeded with Pf1,a = 0.001, and the allowable deflection d with Pf2,a = 0,001.
The simulations were performed using the Ant-Hill program [5]. The starting height h was 80 mm. Then, it was gradually increased with respects to the results of the simulations (100000 trials for each height). The main results are given in the table below. The failure probabilities were calculated via the distribution functions of the pertinent quantities.
h (mm) yave (mm) ymax (mm) M/My ave M/My max Pf1(M>My) Pf2(y>5mm)
80 6.83 9.45 0.632 1.024 0.0004 0.9968
90 4.81 6.65 0.497 0.833 0.0000 0.3486
95 4.10 5.56 0.447 0.750 0.0000 0.0143
100 3.51 4.96 0.403 0.712 0.0000 0.0000
The suitable height of the cross section, fulfilling both conditions, is h = 100 mm. The table illustrates the importance of the choice of the reference value and probability of its exceeding. If, for example, the allowable deflection were 6 mm, or if the permitted probability of exceeding the deflection 5 mm were 1.5%, the height h = 95 mm would be sufficient.
The table also shows the average and maximum values obtained in the simulations (subscripts ave and max). When studying the reliability, one should consider not only the probability of exceeding the pertinent limit state, but also the possible extreme values (obtained in the simulations). If they do not differ much from the „limit value“, the allowable probability of „failure“ may be higher than if the (improbable, but possible) extreme value can significantly exceed the limit value - with respect to the consequences of this exceeding.
3 Example 2 - dynamic loading, extreme situation
In this case, the beam is struck in the middle of the span by a moving body. Some plastic deformations are allowed, but only so that the permanent deflection after unloading does not exceed a permitted value. Also, plastic collapse is not allowed. These two conditions represent limit states. Again, the mass and velocity of the body, as well as the dimensions of the cross section and yield strength of the beam are random variables, so that some very small probability of exceeding the limit values will be permitted.
The role of the beam is to absorb the kinetic energy of the moving body. The body acts on the beam by the force F and deflects it. The kinetic energy of the body changes into the energy of elastic strains in the beam and, possibly, into the work of plastic deformations. Thus, it is first necessary to calculate the kinetic energy of the moving body, U = mv2/2, where m is its mass and v is the velocity of impact. Then, the maximum force can be determined from the relationship between the force and energy. Then, the total deflection is obtained from the F(y) relationship. These calculations depend on whether the deformations are only elastic or elastoplastic. In the latter case, the permanent deflection after unloading is calculated as the difference between the total (elastoplastic) deflection, and the deflection caused by the same force F if the beam deformed only elastically.
The weight of the moving body can also play a role if additional potential energy is released by its movement in the gravitational field due to the beam deflection. For simplicity, however, these effects are not considered in this example (a rigid body moving in horizontal direction). Further, a beam of an ideal elastic-plastic material (without strain-hardening) and rectangular cross section (width b and height h) will be assumed.
For this case, the relationships between the load and deflection are known. The elastic deflection is given by Eq. (4), and the stress is given by Eq. (1). The beam deforms elastically until the maximum stress reaches the yield strength fy of the material. The corresponding force and deflection are
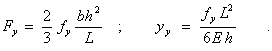 . (5)
. (5)
For higher loads, the maximum stress remains constant (a material without strain hardening), while the plastically deformed region grows. At the ultimate load,
Fu = 1.5 Fy = fy bh2 / L , (6)
the whole cross section in the middle of the beam is plastified (a plastic hinge has been formed). Any further increase of the load would cause a collapse.
The theory of elastoplastic deflections is more complex (see, e.g., [6]). In order to get more general formulae, we first introduce relative (nondimensional) quantities [7]
F* = F / Fy , y* = y / yy , (7)
where F and y are actual values, and Fy and yy are the values at the transition between elastic and plastic deformations, given by Eq. (5). Then, with respect to Eq. (4), the relative elastic deflection (for 0 £ F* £ 1) can be expressed as
y* = F* . (8)
The elastoplastic deflection (for 1 £ F* £ 1.5) can be expressed [5] as
y* = [5 -31/2(3 + F*)(1 - 2F*/3)1/2] / F*2 , (9)
The accumulated (and dissipated) energy U can be obtained by integration of the F(y) relationship. For elastoplastic deformations, the integration must be performed numerically. For generality, relative (nondimensional) energy U* will be introduced, defined here as the ratio of the deformation work corresponding to force F and the work corresponding to Fy:
U* = U / Uy = òFdy / Uy = òFyF* yydy* / (Fyyy/2) = 2 ò F*dy* . (10)
Remark. The constant 2 may seem strange. Actually, the relative energy could also be defined as U** = òF*dy*. In this case, however, the relative energy at the elastic-plastic transition would be U** = 1/2. The difference between both definitions is formal and makes no problems when returning to absolute numbers.
Having the U*(F*) values, the expressions for determining the force from energy can be found. For elastic deformations (0 £ F* £ 1, or 0 £ U* £ 1), the relationship
F* = Ö U* , (11)
is exact. For the elastoplastic range (1 £ F* £ 1.5, or (1 £ U* £ 4.333), there is no explicite analytical expression. An aproximate expression can be obtained by fitting the data by a suitable regression function. A relatively good approximation (coefficient of determination R2 = 0.9997) is
F* = 0,3308 + 0,8806U* - 0,2278U*2 + 0,0201U*3 ; (12)
a polynomial of fourth degree gives even a better approximation. The relative residual deflection, arising for 1 £ U* £ 4.33, can be expressed (with R2 = 0,99996) as
yres* = 0.1467 - 0.2847U* + 0.1508U*2 - 0.0126U*3 . (13)
Remark. Expressing the quantity of interest (here the force F* or residual deflection yres*) by means of a regression function fitted to computer-obtained data for several values of one or more input quantities (here the energy of impact U*) corresponds to the Response Surface Method. Similar approach can also be used for much more complex structures, where the data for the response function can be obtained by the finite element method only. The use of relative (nondimensional) quantities, Equations (7) - (13), leads to more general results, valid not only for one structure, but for a whole class of similar objects. More about the response surface method and the use of dimensional analysis can be found in [7].
The Monte Carlo procedure is as follows. First, random numbers are assigned to the geometric quantities and yield strength of the beam, and also to the mass and velocity of the moving body. Then, the characteristic values Fy and yy for this particular case are calculated, and also the energy U of impact and the characteristic value Uy = Fy yy /2. Then, the relative energy U* is calculated. If U* £ 1, the deformations are only elastic. If U* > 1, the corresponding force F* and relative residual deflection yres* are calculated from Equations (12) and (13).
Two limit states will be considered here: 1) unacceptable magnitude of permanent deflection after the impact, and 2) creation of plastic hinge. The permanent deformation should not exceed some value d, given in mm. Thus, each relative value yres* obtained in Monte Carlo simulations from Eq. (13) must be converted into absolute value yres = yy ´ yres*, which is then compared with d. The probability of failure is calculated as the ratio of the number of cases where yres has exceeded d, to the number of all Monte Carlo trials. The plastic hinge is formed when bending moment attains the ultimate value Mu = 1.5 My. For higher safety, however, the pertinent limit state can be characterized by some fraction of Mu. As the bending moment is directly proportional to the force F and to F* as well, it is sufficient to compare the calculated relative value F* with some number k (< 1.5). Moreover, F* is related to the relative energy U*, see Eq. (12), and it is thus also possible to check this limit state simply by comparing the calculated U* value with the value K = U*(F* = k). Note that U* depends on the load (mass and the velocity of the moving body) as well as on the parameters of the beam (b, h, L, sy).
The reliability conditions for both limit states can be expressed as
RC3 = d - yres > 0 , RC4 = U* £ K , (14)
In this example, the allowable permanent deflection after the impact is d = 1 mm, with permitted probability of exceeding Pf3,a = 0.001. The allowable maximum force is 0.9Fu, which corresponds to k = 0.9´1.5 = 1.35 and K = 2.042, with the permitted probability of exceeding also Pf4,a = 0.001. (The actual ultimate limit state would be characterized by Mu, Fu, k = 1.5 and K = 4.333).
The parameters of input variables (distribution, mean, standard deviation) used in the Monte Carlo simulations are: the mass of the moving body m (normal, 500 kg, 50 kg), its velocity v (normal, 1 m.s-1, 0.1 m.s-1), width of the cross section b (normal, 50 mm, 0.3 mm), the span L (constant, 2000 mm), elastic modulus E (constant, 210 000 Mpa), yield strength fy (steel S 235, the histogram given in [4], with the minimum and maximum values 200 MPa and 395 MPa). The quantity to be found is the beam thickness h in the force direction; it can be chosen from the nominal values 100 - 110 - 120 ... (steps 10 mm). The actual thicknesses have normal distribution, with standard deviation 0.5 mm.
The simulations were performed using the Ant-Hill program [5]. The starting beam thickness was 100 mm, and was gradually increased with respect to the results of simulations. For each height, 100000 steps were made. The standard normal variable u, used in generating the quantites m, v, b, h, was bounded by the interval u = ± 3,5.
The main results are shown in the table below. Umax* and yres, max give the maximum values obtained in the simulations; the value of U* = 4.333 corresponding to plastic hinge.
h (mm) Pf3(yres>1mm) yres, max (mm) Pf4(U*>2.042) U* max
100 0.0256 5.155 0.0591 4.501
110 0.0081 2.792 0.0301 3.404
120 0.0022 2.291 0.0152 3.289
130 0.0006 2.158 0.0073 3.382
140 0.00006 1.265 0.0033 2.797
150 0.00001 0.926 0.0022 2.631
160 0.00001 1.140 0.0006 2.865
The condition of acceptable permanent deformation Pf3(yres>1mm) < 0.001 is fulfilled for the height 130 mm (however, with the maximum value in the 100000 simulations yres, max = 2.16 mm and unacceptably high probability of exceeding the relative energy of impact U* = 2.042, corresponding to 0.9 Mu). The condition P(U*>2.042) £ 0.001 is fulfilled only for h ³ 160 mm. Thus, the beam height satisfying all conditions is h = 160 mm. The results also illustrate the importance of a thorough analysis and a proper choice of limit values. Notice also that some extreme values obtained in the simulations do not decrease monotonously with increasing height.
4 Discussion and conclusions
Reference values quantitatively characterize limit states. Due to probabilistic character of input quantities, the reference values can be exceeded with some small probability. The probability of failure in reliability assessment is not the probability of actual collapse, but the probability of exceeding the (suitably chosen) reference value. The allowable probability of failure should depend on the probability of the event leading to the failure and on the consequences of failure.
The illustrative problems analysed in this paper were very simple, with explicit analytical relationships between the load and deflection. However, the procedures used in the Example 2 (obtaining the analytical relationships between the impact energy and the contact force or residual deflection by fitting a group of values by a regression function) correspond to the Response Surface Method, suitable for the Monte Carlo analysis of complex structures.
Acknowledgment
This work was done as a part of a research project supported by the Grant Agency of the Czech Republic (No. 103/01/0243), and of the Jan Perner Transport Faculty research project MSM 255100002.
References
[1] Marek, P., Guštar, M. and Anagnos, T.: Simulation-based reliability assessment for structural engineers. CRC Press, Inc., Boca Raton, Florida 1995.
[2] Marek, P., Brozzetti, J. and Guštar, M. (editors): Probabilistic assessment of structures using Monte Carlo simulation. ITAM Academy of Sciences of Czech Republic, Prague, Czech Republic, 2001.
[3] Menčík, J.: Reference values (Safety, Serviceability and Durability). Proc. Int. Coll. Euro-SiBRAM’2002, ITAM CAS, Prague, 2002, Vol. 1, pp. 38-39.
[4] Tikalsky, P.: Reference Values for Durability Based Performance Design Criteria. Proc. Int. Coll. Euro-SiBRAM’2002. ITAM ASCR, Prague, 2002 pp. 36-37.
[5] Guštar, M. and Marek, P.: Ant-Hillâ computer program for Monte Carlo simulations. ARTech, Prague, 2001.
[6] Šmiřák, S., Bažant, Z., Kolář, A. and Svoboda, M.: Theory of plasticity and limit states (In Czech, Teorie plasticity a mezních stavů). VUT, Brno, Czech Republic, 1966.
[7] Menčík, J.: Use of response surface method in reliability assessment of transport structures. Proc. Int. Conf. Reliability and Diagnostics of Transport Structures and Means 2002. University of Pardubice, Pardubice, 2002, pp. 200-207.