Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic
Session 3
Accidental loads: codification of simulation-based procedures for predicting load characteristics
Abstract
This paper explains an application of stochastic simulation to predicting characteristics of accidental loads. It is stated that the stochastic simulation is suitable to generate statistical samples of the characteristics through mathematical modeling of accidents involving possibility of imposition of the accidental loads. It is suggested that the modeling should be based on Bayesian approaches to uncertainty quantification. Problems of codifying application of the Bayesian approaches to load predicting are considered in short.
Key Words: Accidental load, stochastic simulation, uncertainty, Bayesian approach, codification.
1. Introduction
Accidental loads and, more generally, accidental actions are dangerous physical phenomena which, if occur, can cause considerable damage to structures and non-structural property. In most cases, accidental loads are of short duration, and a nomenclature of such loads is, in principle, well-known for structural engineers [1, 2].
Physical phenomena resulting in an imposition of an accidental load and circumstances of their occurrence can carry a good part of uniqueness and characteristics of the load can be influenced by a large number of uncertain factors. The uniqueness of an imposition of the accidental load and/or structural exposure to the load can cause that a choice of mathematical models for the load, deterministic or probabilistic, should be done on the basis of sparse statistical data on its occurrences. In some cases, direct measurements of load characteristics can be unavailable at all.
Shortage or absence of statistical data renders a pre-setting characteristic values of the accidental loads in the manner usual for normal loads (loads acting during normal service conditions of structures) impossible. The same pertains to fitting probabilistic models of the accidental loads. Because of this, an attempt to provide the structural engineer with certain means of obtaining values of the accidental loads applicable in the design process can hardly be based on the classical scheme of collecting a relatively large amount of data on load occurrences and processing the data to the form of some characteristic values or probabilistic models. An alternative approach should be fixed in design codes for the choice of mathematical models (characteristic values) of the accidental loads.
Fig. 1 Data collection and processing in two extreme cases of mathematical load modeling: normal load backed by sufficient amount of statistical data (a) and accidental load with a low likelihood of imposition (b)
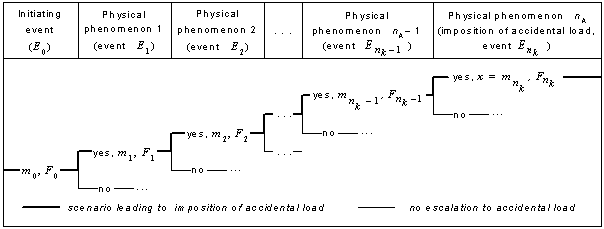
Fig. 2 Event tree representation of an accident leading to an imposition of accidental load and models comprising mathematical model of the entire accident
2. Simulation-based generation of data on accidental loads
Mathematical models of accidental loads can be chosen on the basis of simulation-based modeling courses of accidents which lead to an imposition of accidental loads [3, 4]. The modeling can produce simulated statistical samples to which the mathematical models, deterministic or probabilistic, can be fitted. The simulation-based modeling can to some extent replace physical experimentation with or observation of the process of load imposition (Fig. 1).
A prerequisite of an application of the simulation-based modeling courses of accidents are mathematical models of physical phenomena sequences of which lead to an imposition of accidental load. The event tree (logical model of an accident) shown in Fig. 2 includes a path (accident scenario) escalating into an imposition of an accidental load with characteristics expressed by the vector x. The set of the mathematical models related to the event tree path (accident model) can be represented in the schematic form
with elements explained in the
Table. The last model yields characteristics of the accidental load,
that is,
(Fig. 2).
The simulation-based modeling
consists in a computation through the models
(k = 0, 1, … , nk)
repeated n times. Each repetition differs from others by
different simulated values of model input and output. What is more,
each individual repetition does not necessarily lead to an imposition
of the accidental load (event
).
The main result obtained from the n repetitions of the
simulation is a sample of characteristics of the accidental load,
x1, x2, … , 
,
where the sample size na is the number of
impositions of the accidental load in n occurrences of the
initiating event E0 (na £ n).
The relative frequency na/n can be used to
estimate the conditional probability of imposition of the accidental
load given an occurrence of the initiating event E0,
that is, the probability
.
A choice of the elements of the
accident model X can generally face
the entire range of problems of accident modeling encountered in the
quantitative risk assessment (see discussions in Refs. [5, 6]).
The most important problem, which penetrates the entire QRA, seems to
be handling uncertainty related to an occurrence of the events Ek
(k = 0, 1, … , nk)
as well as models
and
.
A solution of this problem requires to use properly objective
statistical data and subjective expert opinions related to the models
of the physical phenomena as well as to collect and process this
information in the way, which can be fixed in a design code and so
uniformly applied to a design of structures exposed to danger of
accidental loads.
3. Bayesian approaches to handling uncertainty related to accidental loads
Two approaches to handling
(modeling) the uncertainty, namely, the classical Bayesian approach
(CBA) and pure (fully) Bayesian approach (PBA) were suggested and
widely discussed in the field of the quantitative risk assessment
[7, 8]. As applied to the problem of the simulation-based
predicting characteristics of accidental loads, CBA and PBA can be
considered as approaches allowing to combine objective statistical
data related to occurrences of the events Ek (k =
0, 1, … , nk) as well as models of
corresponding statistical phenomena,
and
,
with expert opinions on the branching probabilities
P(Ek | E0 ÇE1 Ç… ÇEk–1)
and the models and/or their parameters. The expert opinions are
understood as “uncertainty of the analyst” or “analyst
degree of belief” and are called the epistemic (reducible)
uncertainty (columns 3 and 4 in the Table).
The approaches allow, at least in
principle, to perform Bayesian updating of the models used to express
epistemic uncertainty. In the beginning of the load prediction, the
c.d.f.s
used
in CBA and the c.d.f.s
and
applied
in PBA express a priori information including expert opinions.
Additional knowledge will decrease the epistemic uncertainty
expressed by the c.d.f.s. What is more, CBA and PBA do not break down
when objective statistical data on some of the physical phenomena are
not available at all.
|
Table. Elements of the accident model X |
|||||||
|
Model(1) |
Form and destination of model |
Function of model in uncertainty modeling |
|||||
|
|
|
in CBA(3) |
in PBA(3) |
||||
|
1 |
2 |
3 |
4 |
||||
|
|
joint c.d.f.(2) used to model uncertainty related to
the models
|
models epistemic uncertainty(4) |
models epistemic uncertainty |
||||
|
|
|
joint c.d.f. used to model uncertainty in the input variables of
the model
|
models stochastic uncertainty(4) |
models epistemic uncertainty |
|||
|
|
|
|
set of algebraic equations, differential equations etc. used to
simulate the kth physical phenomenon; yields input values
to the subsequent models
|
not used in uncertainty modeling |
not used in uncertainty modeling |
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
(1) in the models, symbols “z” denote input vectors, symbols “p” denote parameter vectors; (2) c.d.f. = cumulative distribution function; (3) CBA = classical Bayesian approach, PBA = pure Bayesian approach; (4) see definitions of the epistemic and stochastic uncertainty in Refs. [7, 8] |
|||||||
In the framework of CBA and PBA,
the procedure of the simulation-based modeling described in the
previous section can be considered as a mathematical tool for
propagating uncertainty expressed by the c.d.f.s
and
(lower
level uncertainty) up to the uncertainty in characteristics of
accidental load (upper level uncertainty). In principle, no essential
obstacles seem to exist which would not allow to adopt CBA and PBA
for the predicting characteristics of rare accidental loads and to
fix them in design documents, say, design codes for loads.
4. What should be codified?
Application of CBA and PBA to predicting characteristics of accidental loads requires elicitation and use of expert opinions. The number of experts involved in the predicting can be relatively large. The nature of accident which can result in an imposition of an accidental load can generate a need to hire experts on very different fields lying far beyond the traditional structural engineering. Diversity of the fields and need to ensure cooperation of the experts necessitates a formal basis which should allow to unify handling expert opinions. Such a formal basis could be fixed in a design document (code, guidelines, standard) used to design new structures and assess existing structures exposed to danger of accidental loads.
The design document should allow to avoid unacceptable variability in opinions of different experts. It should be also suitable to determine how to document results of the prediction and how to interpret these results. The need of codification of the predicting accidental loads on the basis of CBA and PBA is in many respects closely related to the general problems of documenting results of risk analyses carried out by applying CBA and PBA [7, 8].
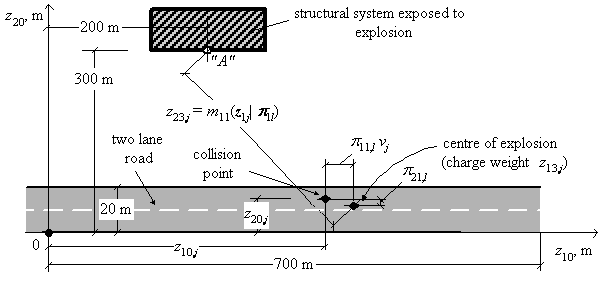
Fig. 3 Accident including an explosion on road
5. Example case study: impulsive load induced by an accidental explosion on road
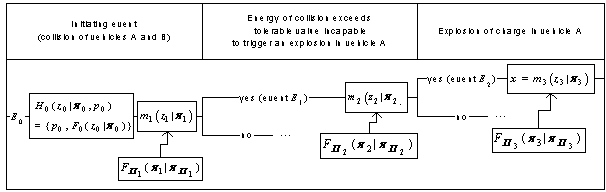
Fig. 4 Event tree diagram with a path leading to an explosion on road
Consider an accident which can occur on a straight section of a two lane road (700 m ´ 20 m road section) (Fig. 3). The accident can be initiated by a collision of a vehicle carrying explosive materials (vehicle A) with a casual opposite vehicle (vehicle B). An explosion can occur in consequence of the collision and impose impulsive load on the structural system build in the vicinity of the road section. A logical model (event tree) of this accident is shown in Fig. 4.
In this case study, a sample of values of the peak positive overpressure x1 and positive impulse x2 of the incident blast wave generated by the explosion is to be created by means of the simulation-based modeling courses of the accident. In addition, the conditional probability of explosion given the collision, P(E1 Ç E2 | E0), is to be estimated from results of the modeling.
In the simulation-based modeling,
the probabilistic model H0(z0|p0, p0) = {p0,F0(z0|p0)}
is used to express via the frequency p0 and the
c.d.f. F0(z0|p0)
stochastic uncertainty related to the likelihood of the initiating
event E0 (collision) and its characteristics,
respectively. The deterministic model m1(z1| p1)
is used to decide whether the energy of collision of vehicles A and B
is sufficient to damage the container with explosive charge and
trigger an explosion as well as to compute the standoff of explosive.
The model m2(z2| p2)
is used to decide whether the energy of collision of the vehicles A
and B when exceeds the safe “threshold” value can cause
an explosion of charge in the damaged vehicle A. The model m3(z3| p3)
is used to relate charge mass and standoff with characteristics of
incident blast wave. Finally, the c.d.f.s
(k = 1, 2, 3)
are applied to express epistemic uncertainty in parameters of the
respective deterministic models
(k =
1, 2, 3). A detailed description of the models can be found in Refs.
[9, 10].
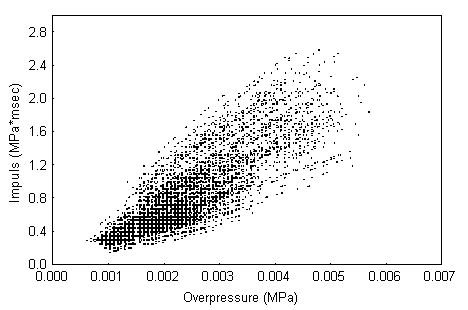
Fig. 5 Scatter diagram of values of peak positive overpressure x1 and positive impulse x2 of the incident blast wave
In this case study, 1´ 106 repetitions of the simulation loop were carried out, that is, n = 1´ 106. The number of explosions counted during the simulation, na, is equal to 55 444. The scatter diagram of the simulated sample containing values of peak positive overpressure and positive impulse, that is, x1, x2, … , x55444, is shown in Fig. 5. With the numbers n = 100 000 and na = 55 444, the conditional probability P(E1 Ç E2 | E0) can be estimated by the ratio 55 444/(1´ 106), that is, as 0.055444. Then the frequency of the explosion can be estimated by the product p0 ´ 0.055444.
6. Conclusions
Stochastic simulation can be applied to a predicting characteristics of the accidental loads which can be imposed on structures during major industrial accidents. The simulation consists in mathematical modeling courses of accident leading to an imposition of the loads. Such a simulation-based modeling can replace in part a direct physical experimentation with and observation of the accidental loads. It is important to take proper account of uncertainty related to mathematical models used to the simulation-based modeling. Two methodological frameworks developed in the field of the quantitative risk assessment, namely, the classical Bayesian approach and the pure Bayesian approach to uncertainty quantification provide a basis for handling the uncertainty.
The predicting characteristics of the accidental loads seems to be the area of the structural engineering in which a combined application of Bayesian approaches and stochastic simulation does not have a valuable alternative in the load predicting by prevailing deterministic methods. The nature of the Bayesian approaches requires that the load predicting on their basis should be fixed in a design document (code, guidelines, standard) which could unify and regulate the predicting and document its preparation and results in a proper form.
References
[1] ISO 2394: 1998(E). General Principles on Reliability for Structures. ISO, Geneve, 1998.
[2] ENV 1991-1: 1993. Basis of Design and Actions on Structures. CEN, Brussels, 1993.
[3] E. R. Vaidogas. Uncertainties Related to Hazard Functions of Accidental Explosions. In: Safety, Risk, and Reliability - Trends in Engineering. Report of Int. Conf. held in Malta. Safety and Risk in Engineering, Zürich, 2001, 495-500 p.
[4] E. R. Vaidogas. Modelling Uncertainties in Assessing Risks to Structures Caused by Accidental Explosions. Civil Engineering, VII, No. 2, 2001, 89-98 p.
[5] G. Apostolakis. The concept of probability in safety assessments of technological systems. Science, Vol. 250, No. 4987, 1990, pp. 1359-1364.
[6] J. Devooght. Model uncertainty and model inaccuracy. Reliability engineering and system safety, Vol. 59, 1998, p. 171-185.
[7] T. Aven, K. Pörn. Expressing and interpreting the results of quantitative risk analyses. Review and discussion. Reliability Eng and System Safety 1998; Vol. 61. p. 3-10.
[8] T. Aven, W. Rettedal. Bayesian frameworks for integrating QRA and SRA methods. Structural Safety 1998;20:155-165.
[9] E. R. Vaidogas. Probabilistic modelling of accidental actions 1: Simulation-based choice of models. A paper submitted to a possible publication in Structural Safety, 2002.
[10] E. R. Vaidogas. Probabilistic modelling of accidental actions 2: Case studies involving simulation of accident courses. A paper submitted to a possible publication in Structural Safety, 2002.