Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic
Session 3
SBRA method as a tool for reliability analysis of structural members exposed to multi-component load effects
Abstrakt
The following study demonstrates on concrete example the potential of SBRA method in reliability analysis of multi-component load effects.
Key Words: SBRA method, random variable, bounded histogram, multi-component load effect.
Today’s codes for design and assessment of building structures are mostly based on semi-probabilistic prescriptive interpretation of Limit State Design method called „Partial Factor Design“ method. These codes define rules for determination of load effects using combination formulas. In case of multi-component load effects according to these codes can be extremely difficult to find critical combination of these load effect, due to insufficient descriptions of individual loads and limited possibilities of these combination formulas (see [4]).
Simply and efficient way of multi-component load effects determination offer fully probabilistic method SBRA (Simulation-Based Reliability Assessment) documented by Marek et. al. [1], [2], [3]. The following study demonstrates on concrete example an analysis of normal stresses in fixed column using the SBRA method [5].
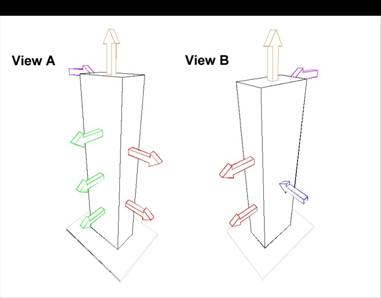
Goal of the study is finding the position of maximum compressive normal stress sx in fixed column of the rectangular cross-section (see Fig. 1 and Fig. 2). The column is exposed to system of random variable forces. For considered position and selected probability P = 0,00007 has be found a such „equation“ in 3D space, whose every point will represent just one combination of normal force Nx and bending moments My and Mz. Individual random variable loads used in the following calculation are shown in Tab. 1. Used bounded histograms representing variabilities of these loadings are shown in Fig. 3. Geometrical properties of the structure are considered by nominal values (see Tab. 2).

Fig. 1 System of random variable forces acting on vertical column fixed in the foot (perspective views)
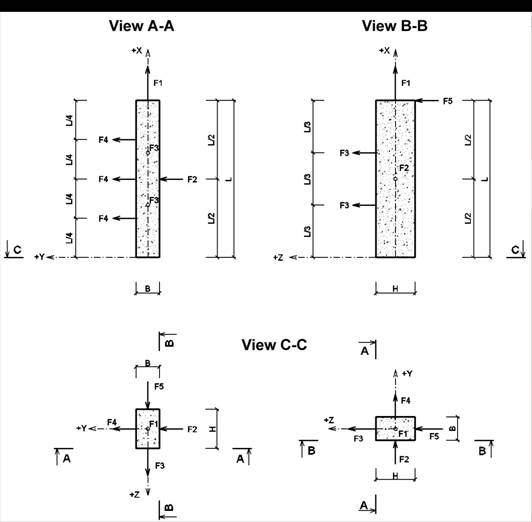
Fig. 2 System of random variable forces acting on vertical column fixed in the foot (orthogonal views)
Tab. 1 Maximum values and corresponding bounded histograms of loads
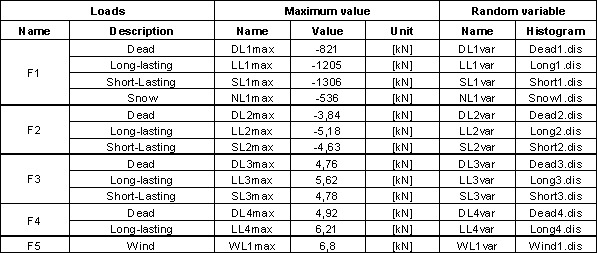




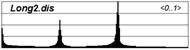







Fig. 3 Used bounded histograms of random variable loads
Tab. 2 Nominal values of geometrical properties

In the study is considered ideal elastic behaviour of structure and transformation model corresponding to 1st order theory. In case of elasto-plastic response of the structrure and applying of transformation model based on 2nd order theory can be applied the same approach, howewer multi-component load effects will be affected by deformation of the structure.
Effects of random variable loads in arbirtrary position of the structure (in case of shear forces neglecting) can be expressed by normal stress:
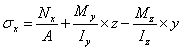 ,
(Pa) (1)
,
(Pa) (1)
where Nx, My and Mz represent three components of internal forces (normal force and bending moments to corresponding axes – see [6]).
Equation of a „plane“ in 3D space, which for arbitrary position of any cross-section and for selected probability P represents infinity number of three-component load effects combinations (normal force Nx and bending moments My and Mz), can be expressed by the equation:
![]() ,
(Pa) (2)
,
(Pa) (2)
where a = 1 / A, b = z / Iy, c = y / Iz. Quantity d represents magnitude of normal stress sx in considered position of considered cross-section.
By the calculation was found, that maximum compressive normal stress in considered member is in the foot of the column in position of coordinate [0;B/2;H/2] (see Fig. 2). For this position and for selected probability P = 0,00007 was found (according to the equation (2) „plane“ in 3D space, which represents infinity number of combinations of normal force Nx and bending moments My and Mz. This „plane“ is shown together with „3D anthill“ in Fig. 4 (perspective views from various directions).
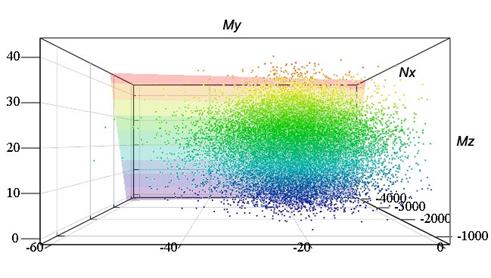
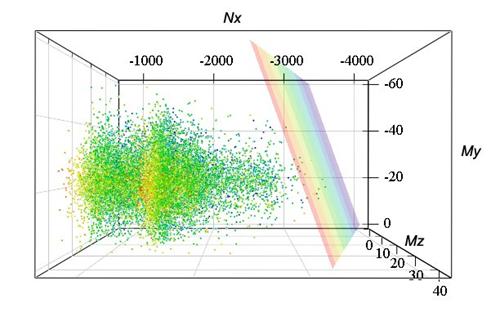
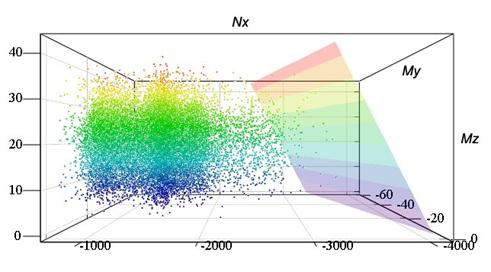
Fig. 4 „3D anthill“ and „plane“ representing infinity number of combinations of load effects of Nx, My and Mz
This study demonstrates the analysis of multi-components load effects for three components of internal forces – normal force Nx, bending moment My and bending moment Mz. This approach can be summarized into these points:
(a) Three-components combinations of load effects can be expressed by „3D anthill“ (see Fig. 4), where every point represents just one random sampling of combination of normal force Nx and bending moments My and Mz.
(b) „3D anthill“ can be interlayed by selected „plane“ and consequently can be determined a probability of occurence of points on one side from considered „plane“ (sum of points on one side divided by sum of all points).
(c) According to the equation (2) can be for arbitrary position of any cross-section of analyzed structure determined such a „plane“ (Nx, My, Mz), where to each its point coresponds equal normal stress sx in the considered position of the cross-section.
(d) Various parallel „planes“ correspond to various probabilities of exceedance of normal stress sx (see paragraph (b)) in considered position of the cross-section.
(e) For selected probability P can be determined (in considered position) corresponding normal stress sx using iterative procedure (see AntHillÔ for DOS).
Demonstrated appoach can be partly used to determination of normal stress sx in considered position corresponding to selected probability P as well to determination of probability of failure Pf. Analogically to this approach can be for four- and multi-component load effects constructed four- and multi-dimensional „above anthill“ for determination of stress corresponding to the selected quantile.
Today’s codes do not contain instructions which values of Nx, My, Mz should be applied in the equation in a such way, so that the probability of combination will be respected. Interaction formulas introduced in contemporary codes do not lead to determination of one critical combination, but to infinity number of combinations meet the conidition (2). Thus, the application of interaction formulas used in analyses of multi-component load effects according to today‘s codes cannot lead to consistent and satisfactory results.
The support of the Grant Agency of the Czech Republic (Projects No. 103/01/1410 and 105/01/0783) is gratefully acknowledged.
[1] Marek, P., Guštar, M., Anagnos, T.: Simulation-Based Reliability Assessment for Structural Engineers. CRC Press Inc., Boca Raton, Florida, 1995.
[2] Marek, P., Guštar, M. a Bathon, L.: Tragwerksbemessung. Von deterministischen zu probabilistischen Verfahren. Academia, Praha 1998.
[3] Marek, P., Brozzetti, J., Guštar, M.: Probabilistic Assessment of Structures using Monte Carlo Simulation. Background, Exercises and Software. Institut of Theoretical and Applied Mechanics, Academy of Sciences of the Czech Republic, Praha, 2001.
[4] Krejsa, M., Marek, P.: Ověření spolehlivosti ocelové konstrukce pravděpodobnostním výpočtem. Část 5 - příklad dimenzování při vícekomponentních účincích zatížení. Stavební obzor, s. 54-58, roč. 8, č. 2, 1999, ISSN: 1210-4027.
[5] Pustka, D., Disertation work: Využití spolehlivostní metody SBRA při navrhování ocelových, betonových a ocelobetonových konstrukcí. VŠB – Technical University of Ostrava, Ostrava, September 2002.
[6] Šmiřák, S.: Pružnost a plasticita I pro distanční studium. Akademické nakladatelství CERM, s.r.o. Brno, 1999, ISBN 80-214-1151-1.