Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic

Session 3

Multi-component representation of crane-girder loading

Professor Ing. Ján Hudák, PhD.

Technical University Košice, Slovak Republic

1. Introduction

Initiation and propagation of cracks caused by variable repeated load-effects characterize the fatigue process. The fatigue process leads to progressive failure and total diminution of the service life of the loaded components of structures. Decisive factors, which determine this process are loading history and corresponding load effects history, geometrical form of structure, configuration of details, residual stresses due to rolling and/or welding etc., and eventually defects and stress concentrations. The primary influence on the fatigue damage and failure, considering the mentioned effects and factors have, first of all, the load effects  history, stress concentrations and residual stresses.

In the aspect of the solution of problem fatigue loading and stress using probabilistic approach is necessary to give attention to the analysis of loading and of the response of the structure to the loading. The result of this analysis is determination of the response spectrum, which was created by statistically modeling the pay-load Q together with the  position of the crab  within the span of the crane , with limiting lengths in the ended parts . For dispersion variance of intensity of loading in the investigated range and density character of probabilistic incidence is represented by histograms (see Figure 1). We can proceed by the same method in order to determine the  crab position histogram on the crane bridge.  From this two quantities, which characterize magnitude of load and its position by using of transformation model of simple beam are determined its support reactions for random chosen quantities from loading spectrum  and crab position . By these supporting reactions are determined components of wheel loading spectrum of crane, which by this way concisely can characterize the response of the structure to the crane-load history. 

The value, which enters the reliability condition, is loading effect as the result of interaction of loading and transformation model of structure. Transformation model of structure is suitable to elect in the form of influence line of static quantity, which is investigated. The time diagram of loading effect for determined period of working shift, eventually for time of one year, we obtain by moving on the influence line of system of loading, which is introduced by chosen wheel loading  from the loading spectrum.

2.   Modeling of loading

For demonstration of introduced problem we will contemplate the crane way girder in industrial hall of 30 m span and span of columns 6 m. In the hall are working two cranes with carrying capacity 50  and 32 , width supposing 100 crossing per working shift. The aim of task is to determine probability failure of steel girder  from the point of view of fatigue loading caused by normal stress in the lower part of girder in the middle of its spoon.

Geometrical dimensions of welded steel girder with high 1050  made from steel S235 were determined by preliminary analysis.

At preparation of introduced characteristics of tracing values of loading we use known nominal value of carrying capacity of loading . Dispersion variance of this value by using statistical analysis is possible to consider according to loading coefficients  in range

and also .  Ended values of crab-crane position are determined by value  distance especially by value  and , where  is spoon of crane bridge. There are vectors  and  which are generated by application of histograms, which are similar to statistically distribution for range of minimally and maximally values. After this preparation is possible to find necessary elements of introduced vectors.

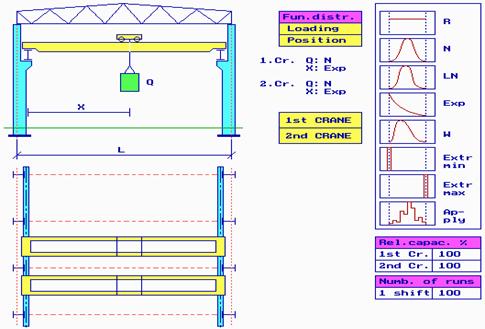
Fig. 1   Selection of histograms similar to statistically distribution for loading   and crab-position

For optional number from file will - element of loading vector  and similarly for  will -element of loading positions vector . There - element wheel loading vector  can be expressed from formula for the reaction of simple beam

,         = 1, 2,  …                                         (1) 

Where  is weight of crane crab,

              - weight of  crane bridge.

The wheel-loading vector will be step by step calculated for , and its form is possible to express as .

2.   Modeling of loading effects

The time course of loading effects in the tracing point of crane girder structure is possible to determine by statically transformation model using influence line. The file of quantities for course bending moment diagram can be expressed by discrete values

,           = 1, 2,  …                                                                          (2)

Where    is actual value of loading from wheel of crane,

            -  Ordinate of influence line of bending moment on the crane way girder.

Fig. 2  Vectors of values of loading , crab position and wheel loading

As is next expressed for given geometry of girder and random choose value of wheel loading from created loading spectrum the time diagram of bending moments is determine in elected point of crane way girder. In next step are identified local extremes of bending moments and for these bending moments and designed cross section of crane way girder adequate values of normal stress are calculated.

File of values of determined stress is characterize time course of loading effects for one crossing of two cranes. 

Fig. 3  Bending moments course on the crane way girder at one crossing of  cranes with nominally values of loading

a) Reservoir method                                                                 b) Rain Flow method

Fig. 4  Stress range spectrum  for one crane crossing

Fig. 5  Stress range spectrum for one working shift

Fig. 6  Stress range spectrum for one working year

Discrete values of normal stress are determined from discrete values of bending moments in single peaks of moment’s line 

,           = 1, 2,  …                                                                         (3)

Where   is extreme magnitude in - peak of bending moment line,

            -   Inertia moment of cross section of crane way girder to central axis ,

             -   Coordinate of investigated point on the girder from center of gravity,

             -   Number of extremes in tracing diagram of bending moments.

The introduced process is repeated for given number of crane crossings per working shift. This time course of loading effects in elected point of girder has stochastic characters and it is necessary made of retransform on the equivalents stress range spectrum. The necessary transformation is made using classifying method Reservoir.

3.  Fatigue damage

The fatigue strength at variable repeating loading changes in dependence on number cycles and on configuration of detail. This strength is determined from experimental results in form S-N curve. Code STN 731401 “Design of steel structures” applies three linear curves for normal stress range. The equation of fatigue strength curve is given in form     

                                                                                      (4)

Where     is fatigue strength,

              -   Number of cycles to failure,

              -   Constant, which expresses inclination of fatigue strength curve,

          -  Constant by table 28 in STN 73 1401.

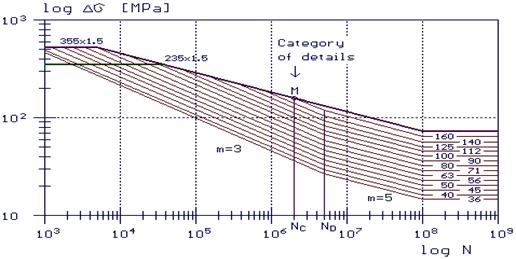
Fig. 7   S-N curves for normal stress range by STN 73 1401

4.  Accumulation of fatigue damage 

We will apply cumulative hypothesis of Palmgren-Miner. This hypothesis is based on the   assumption  that  every  individual  change  of  stress   range  ,  which    multiple    repeating would cause break, will cause damage  ([8]). Total damage is expressed in form

                                                                                                                          (5)

Where  is number of cycles in spectrum for stress range level ,

             - Number of cycles to damage for stress range level .

Table 1 – numerical data of value of spectra from by fig. 6 

If the histograms of number of cycles to damage, which are adequate to stress levels in response spectrum are known, the formulation damage cumulation we can express in the form of vector

                                                                                                                      (6)  

For elected category of detail 100 above given S-N curve for normal stress in table 1 for stress levels from stress range spectrum are determined limits of number of cycles  and  by equation (4).

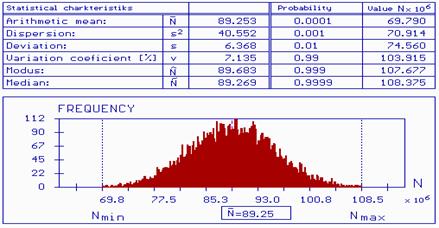
Fig. 8  Histogram and statistical characteristics of number of cycle to damage for stress range level  

Minimal value  is expressed from curve considered detail category 100 and maximal value  is expressed from neighbor upper curve of category detail 112. Considering that stress levels of blocks 1 and 2 are under threshold values, they are not considered in computation of damage cumulation. For upper stress range levels will prepare histograms . After preparing of necessary characteristics we can write vector of damage cumulation

          (7)

Where  is number of years of crane way exploitation.

5.  Reliability assessment   

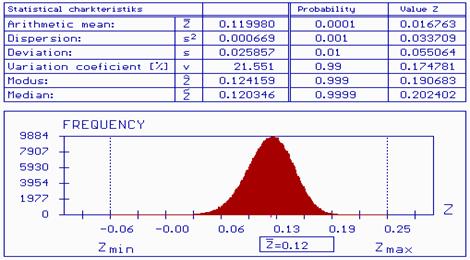
Fig. 9   Histogram and statistical  characteristics of reliability reserve

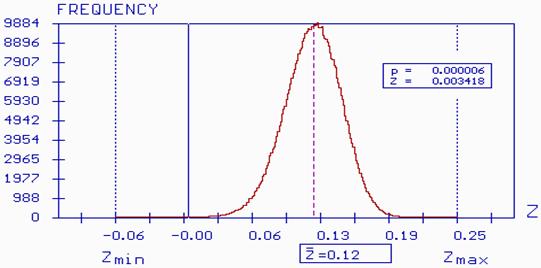
Fig. 10  Marking of probability failure in histogram of reliability reserve 

The reliability structure of crane way from the point of view of high cycle fatigue damage using probabilistic approach [1], [2], [3] [8] we can express function of reserve reliability

                                                                                                                    (8)

Where   is  limit value of damage accumulation, which is given of value 1.

Computation function of reliability reserve is made by M-Star program for 500000 simulation (see fig. 9).

Probability of failure  is calculated by using simulation method Monte Carlo for time of exploitation  =  49,2 years

             =  0,000006  <   = 0,00007                                                                 (9)

 Where   is design value of probability failure by table  A1 in STN 731401.

6.   Conclusions

The application of reliability condition of high cycle fatigue belong to relative complicate tasks from the point of view on various random variable characteristics, which enter from side of loading effect expressed by stress range spectrum and also from the side of resistance of structure expressed by S-N curves. Probabilistic approach using Monte Carlo simulation was applied in the analysis of the load-effects spectrum and also the stress range spectrum using program called CRANE WAY, developed in cooperation with Prof. P. Marek within the framework of an earlier research project. Reliability analysis is based on the SBRA method [1] and M-Star program was used.

REFERENCES

[1] MAREK, P. - GUŠTAR, M. and ANAGNOS, T.: Simulation-Based Reliability Assessment for Structural Engineers. CRC Press, New York, 1996.

[2] MAREK, P. - GUŠTAR, M. and BATHON, L.: Tragwerksbemessung von detrminstischen zu probabilistischen verfahren. ACADEMIA Praha, 1998.

[3] MAREK, P. - BROZZETI  and GUŠTÁR, M.: Probabilistic Assessment of Structures using Monte Carlo simulation. Praha  2001.

[4] HUDÁK, J. - MAREK, P. - VIRČÍK, J.:  Vybrané state z kovových konštrukcií a mostov. Únava a krehký lom oceľových dielcov. ES VŠT Košice, 1987.

[5] HUDÁK, J. - KUĽKOVÁ, E.: Meddling of real loading process and response determination by the simulation on a computer. In: Proceedings of the 2^nd International Scientific Colloquium CAE TECHNIQUES. Bielefeld , 1995.

[6] HUDÁK, J.: Spektrá rozkmitov napätí nosníka žeriavovej dráhy pri posudzovaní na únavu. In.: Zborník „IV. Naukowa konferencja  Rzeszowsko-Lwowska – Problemy budownictwa i inżinierii środowiska“, Rzeszów, 1995.

[7] HUDÁK, J.: K problematike posudzovania spoľahlivosti oceľových konštrukcií na únavu v STN 731401. Inžinierske stavby č. 7-8, Bratislava, 1997.

[8] VLK, M.: Využití simulační metody Monte Carlo při hodnocení životnosti v oblasti vysokocyklové únavy. In.:  Conference  ENGNEERING MECHANICS ´ 95, Svratka 1995.