Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic
Session 3
Two-component wind rosette application
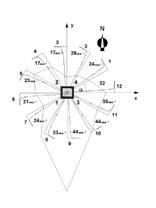
When designing building structure exposed to horizontal wind load, we usually keep this procedure: design it for one direction and then for the opposite direction. But as we know, the wind blows in all directions with different intensity and duration. Using the SBRA method [1], in this example I was engaged in the new wind load effects analysis approach. This time the wind load is expressed by the two-component wind rosette [2] and [3] (see Fig.1), the first component (expressed by a histogram) refers to the duration of the wind in twelve directions and the second component consists of twelve load duration curves (expressed by histograms) corresponding to those directions. The Czech Meteorologic Institute monitor these factors, so it enables us to use it practically.

Fig. 1 - Two-component wind rosette
Imagine a square column footing. It’s proportion and the characteristic values of loads are given: dead load 200 kN, long-lasting load 300 kN, short-lasting load 400 kN and the snow load 100 kN. There is also a wind load given by the rosette. This rosette was obtained from a meteorologic institution. My aim is to determine the pressure under four corners of the column footing and to compare the results.
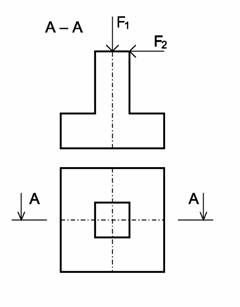
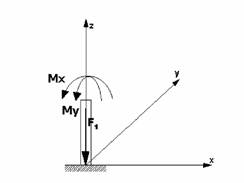
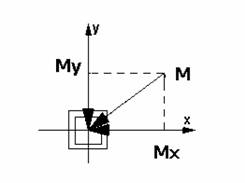
Fig. 2-4 Scheme of concrete block and loading scheme
The wind load is given by the wind rosette. The bending moment in the footing fissure depends on the wind power and the arm of this power. The wind power depends on the wind speed. The constant C represents the arm of wind power and the surface exposed to the wind (C = 0,263222739 kg). Afterwards we get this equation:
![]()
It is necessary to determine the cross-section area and the surface of the column footing for solving our problem. This values could be also probabilistic, but for making it easier the dimension of the footing was set to be constant (B = 1 m).
![]() [m3]
[m3]
![]() [m2]
[m2]
Further the total axial force F is determined. This total force depends on probability and characteristic values of loads and it changes in each simulation step. In the equation indicia F1, F2, F3, F4 represent the histogram and it is multiplied by the characteristic load value:
![]()
In each simulation step I realize in which direction the wind blows. The bending moment of the wind is devided into two parts Mx and My:
![]() [kNm]
[kNm]
![]() [kNm]
[kNm]
Now we have everything to determine the pressure in the footing fissure:
![]() [kPa]
[kPa]
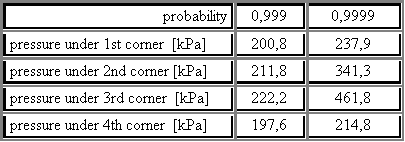
Four pressure values under the footing corners are obtained in each simulation step. The whole process repeats thousand times. Finally the set of those pressures is obtained. The target probability is specified (in this case P = 0,999 and P = 0,9999). The result value is the pressure, that would not be exceeded on the level of target probability. It means that only once in thousand if you like in ten thousand simulations only one pressure is higher than the result presuure.
The result is the pressure under the four corners of column footing (see Table 1). On the target probability level P = 0,999 the result pressure differs from more than 12 %. This is already a significant difference. That is why this method could be profitably used in cases, where the wind load is very important and critical.
Table 1 –Results
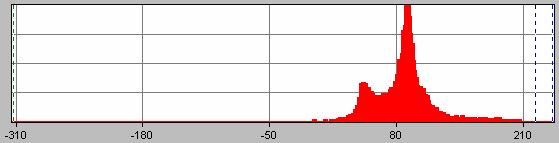
The pressure under the 1st corner.
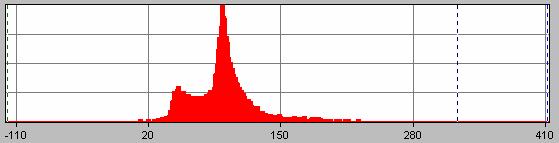
The pressure under the 2nd corner.
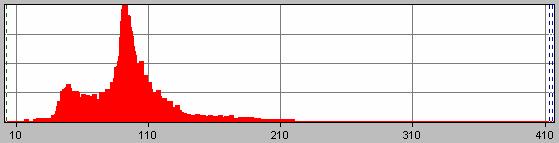
The pressure under the 3rd corner.
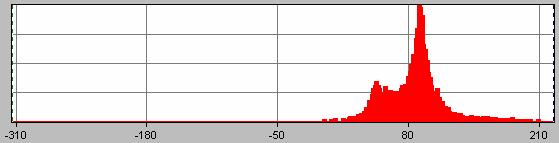
The pressure under the 4th corner.
[1] Marek, P., Guštar, M. and Anagnos, T. (1995). Simulation-Based Reliability Assessment for Structural Engineers. CRC Press, Inc., Boca Raton, Florida.
[2] Němec L. (1990). Rozbor zatížení větrem a sněhem z hlediska aplikace metody Monte Carlo při vyšetřování současnosti odezev na zatížení. Výzkumná zpráva (research report), Sportovní stavby Praha, Czech Republic.
[3] Marek, P., Brozzetti, J., Guštar, M.: Probabilistic Assessment of Structures using Monte Carlo Simulation. Background, Exercises and Software. Institut of Theoretical and Applied Mechanics, Academy of Sciences of the Czech Republic, Praha, 2001.