Euro-SiBRAMí2002 Prague, June 24 to 26, 2002, Czech Republic
Session 3
Loadings representation in SBRA method
Ing. Milan Guštar
ARTech, Nad vinicí 7, 14300 Praha 4, Czech Republic
artech@noise.cz
Abstract
Quantile functions can be used for the representation of random variables. In the SBRA method the quantile function of a load distribution is called the Load Duration Curve - LDC, since its graph shows the duration of individual load values. Non-parametrical form of quantile function is used since most of the loads can not be characterised using simple parametric distributions and their quantile function can not be expressed parametrically.
Key Words: random variable, quantile function, loading, histogram, load duration curve, SBRA.
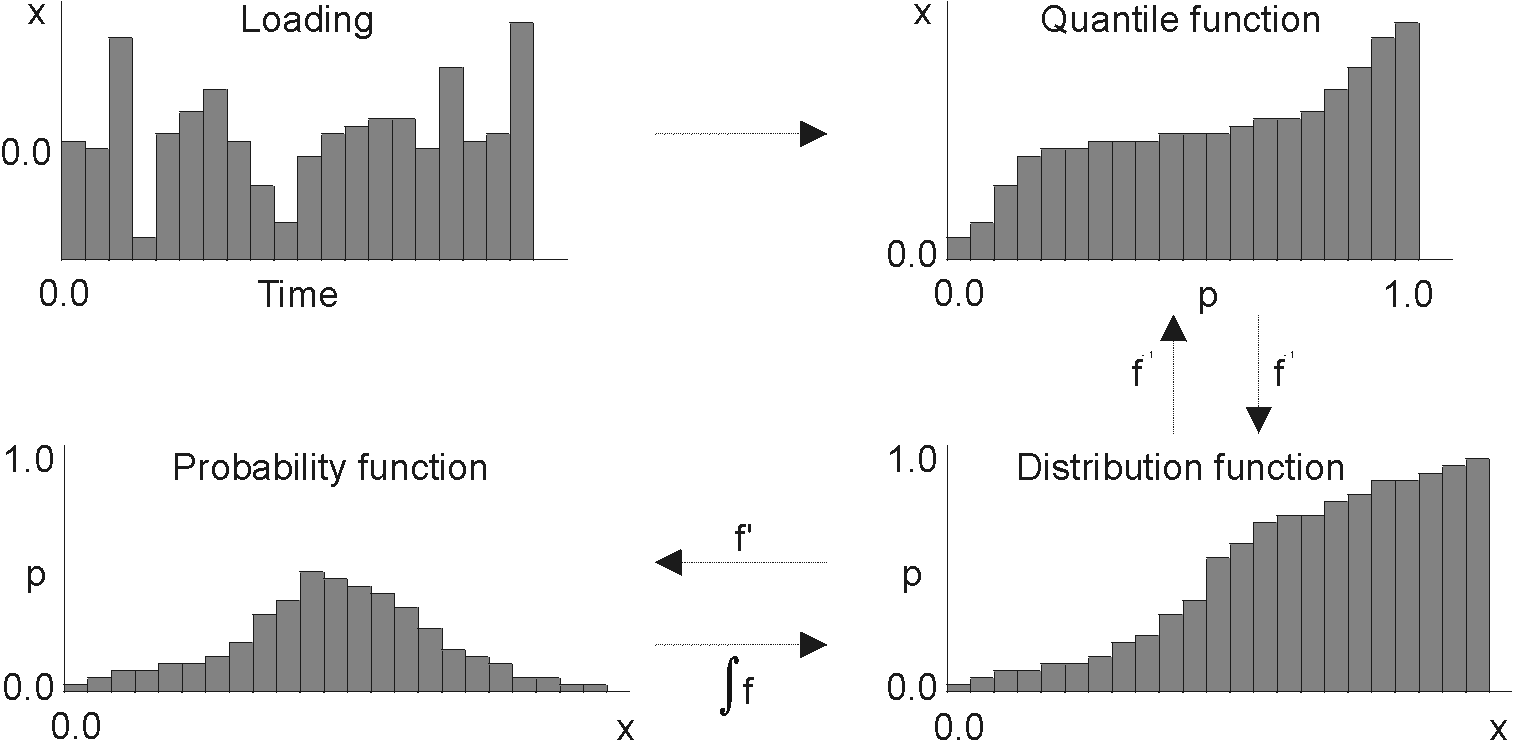
Random variables can be described in various forms. A continuous Probability Density Function (PDF) and a discrete Probability Mass Function f(x) give a natural, easily comprehensible description of the variable distribution. The integral of the probability density function or the summation of the probability masses over all discrete values over the interval (-¥, x0] give the Cumulative Distribution Function F(x0) = Pr[X L x0]. The cumulative distribution function can be used for the assessment that the probability does not exceed a certain value. The Inverse Distribution Function also called the Quantile Function Q(p) = F-1(x) is another form of random variable representation. Using the quantile function, for a selected probability of non-exceedence p, the corresponding value of the random variable can be assessed. The Quantile function can be constructed only for continuous cumulative distribution function, since for non-continuous cumulative distribution function the inverse function does not exist.
The Figure 1 symbolically shows the relationship between described forms of random variables' representation. All described forms of random variables' representation are equivalent and the distribution of random variables is fully characterised by each representation.

Fig. 1: Random variables' representation
Empirical quantile functions can be obtained by sorting, in ascending order, a representative sample over the time a random variable is observed, see Figure 2. In Simulation Based Reliability Assessment (SBRA), the Quantile function of a load distribution is called the Load Duration Curve - LDC, since it represents the duration of individual load values.
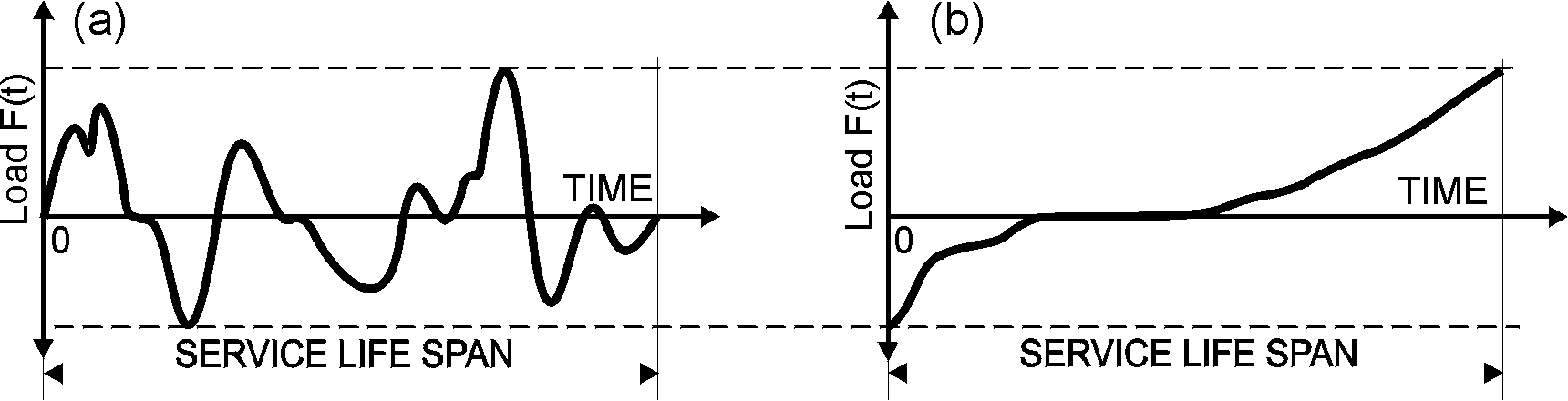
Fig. 2: Load (a) and Load Duration Curve (b)
Non-parametric form is used since most of the loads can not be characterised using simple parametric distributions. Simple distributions can be described using functions in closed form with few parameters. In this case the representation is called parametrical. For more complicated or irregular distributions non-parametrical representation can be used [1], for example in the form of histogram (see Figure 3), polynomial, spline, wavelet, etc.
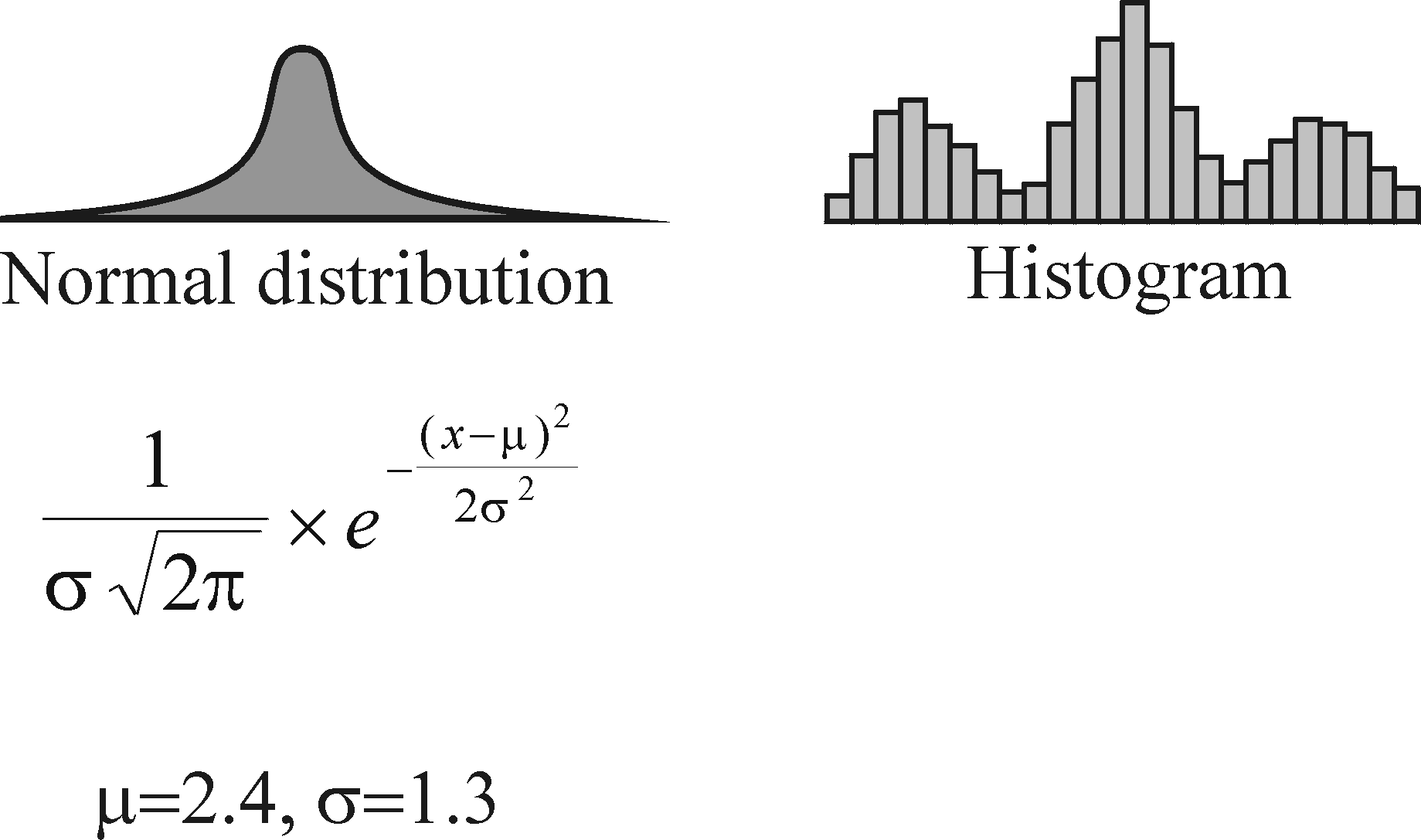
Fig. 3: Parametrical and non-parametrical representation
Many of the load variables (see Figure 4) can not be characterised using simple parametric distributions and their Load Duration Curves (quantile functions) can not be expressed parametrically.
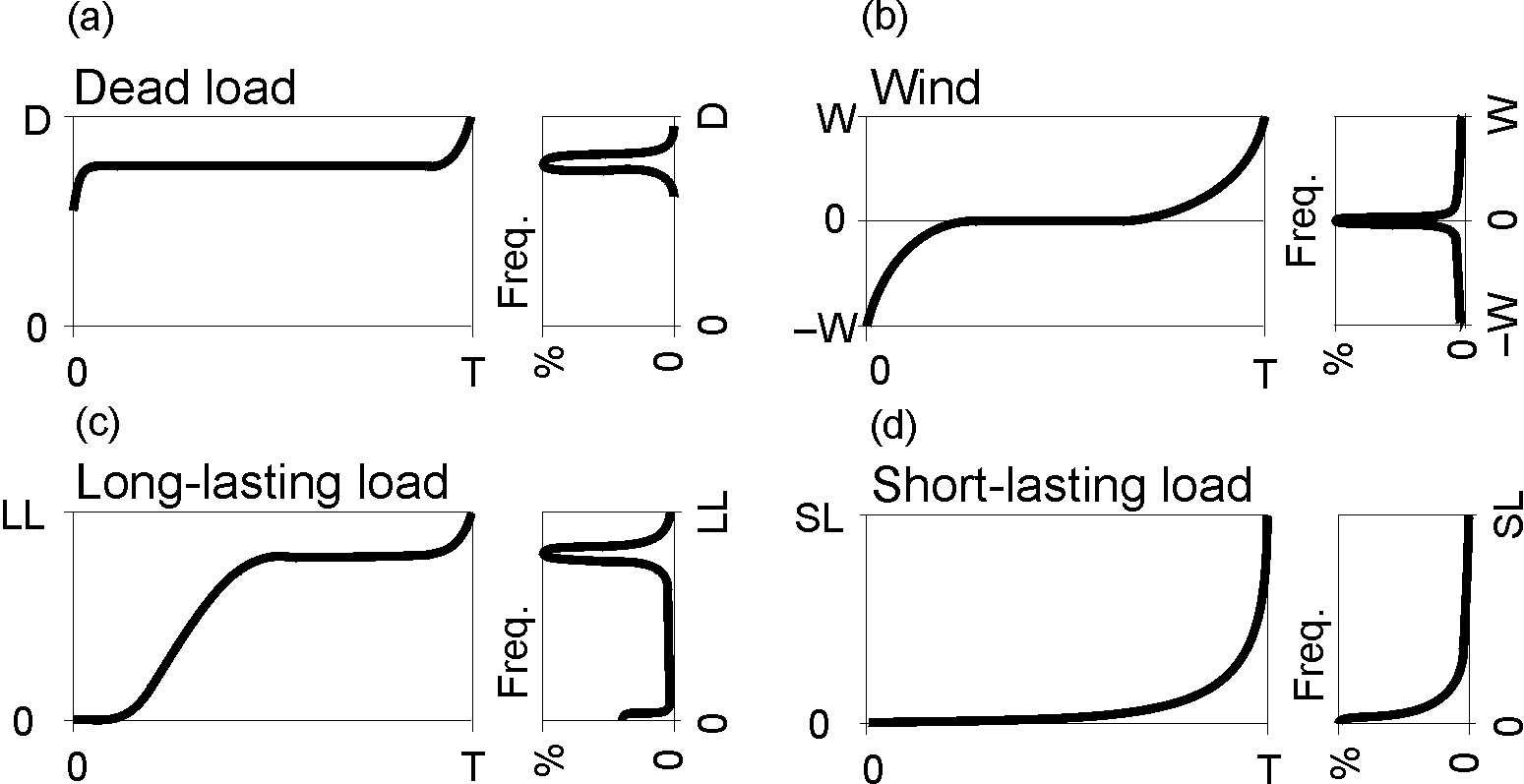
Fig. 4: Loads – LDCs and PDFs
In the SBRA method the histogram is used as non-parametrical form of random variables' representation. According to histogram bins' interpretation, the histogram characterises a piecewise uniform distribution or a general discrete distribution [2].
References
[1] Silverman, B. W.: Density Estimation for Statistics and Data Analysis. Chapman and Hall, 1986.
[2] Marek, P.,Guštar, M.,Anagnos, T.: Simulation-Based Reliability Assessment for Structural Engineers. CRC Press, Boca Raton, Florida, 1995.