Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic

Session 2

Random variables representation in simulation techniques

Ing. Milan Guštar

ARTech, Nad vinicí 7, 14300 Praha 4, Czech Republic

artech@noise.cz

When we take samples of some variable, we observe somewhat different outcomes of observations. In many case we are not able to find all causes of such variation but we can use a probabilistic modeling of the variable which is then called random. The most of variables in simulation methods have more or less random character. Therefore the proper representation of random variables can significantly affect the precision and the speed of the simulation.

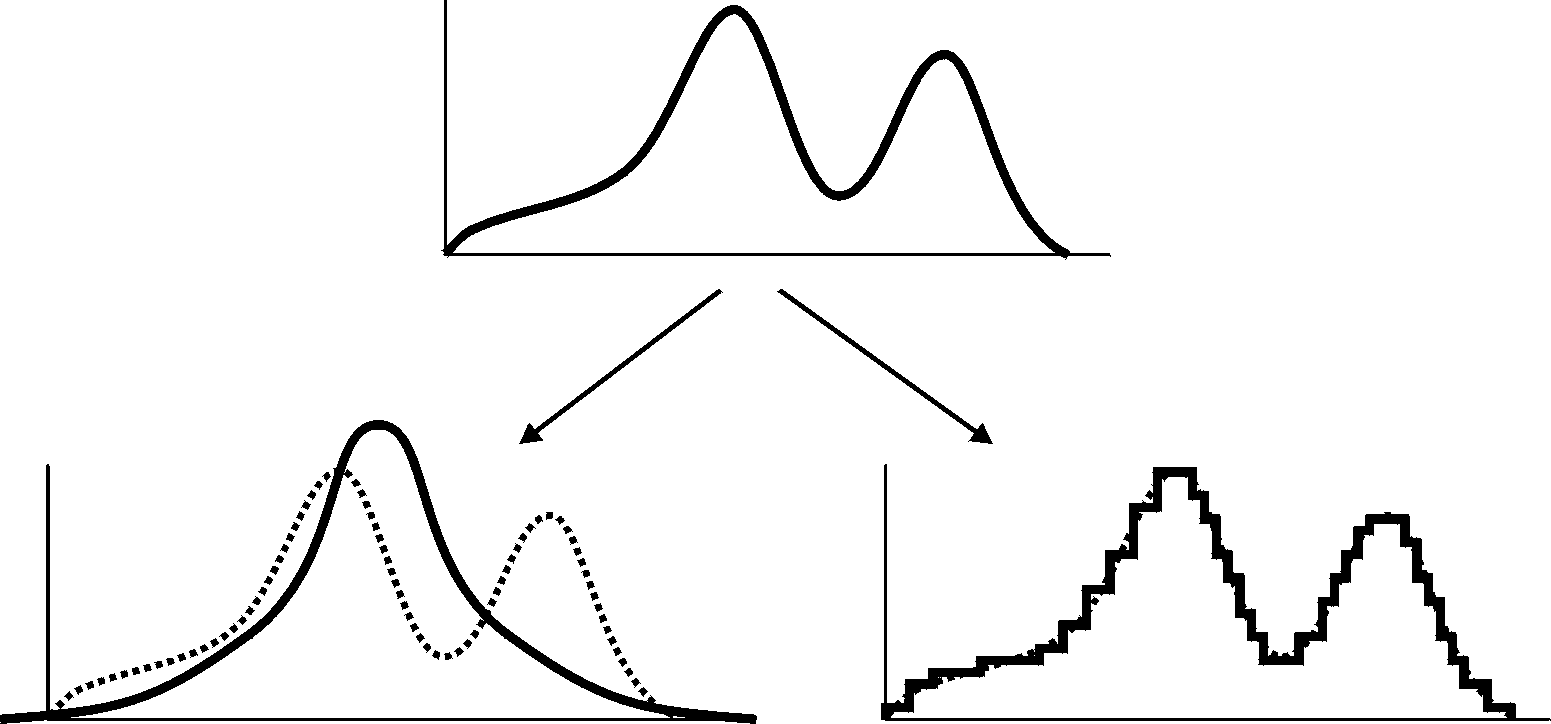
The distributions describing the majority of ”real-life” random variables are not known. The types and statistical parameters of the their distributions are estimated from data obtained from the results of measurements, tests and experiments. From these data a histogram or other non-parametrical distribution is usually created [1] and this empirical distribution is approximated by a selected theoretical distribution. In the cases when correct approximation by the theoretical distribution is impossible, non-parametrical distribution can be used as the approximation of the original distribution, see Figure1.

Fig. 1: Parametrical and non-parametrical distribution approximation

If the histogram is used, the distribution of a variable within individual histogram bins can be assumed to be uniform over the bin. Then the resulting histogram represents a piecewise uniform distribution. If the all values inside individual bins are represented by only one value (for example, at the centre of the bin), the resulting histogram represents a general discrete distribution. For the relationship between the original distribution, piecewise uniform distribution and general discrete distribution see Figure 2.

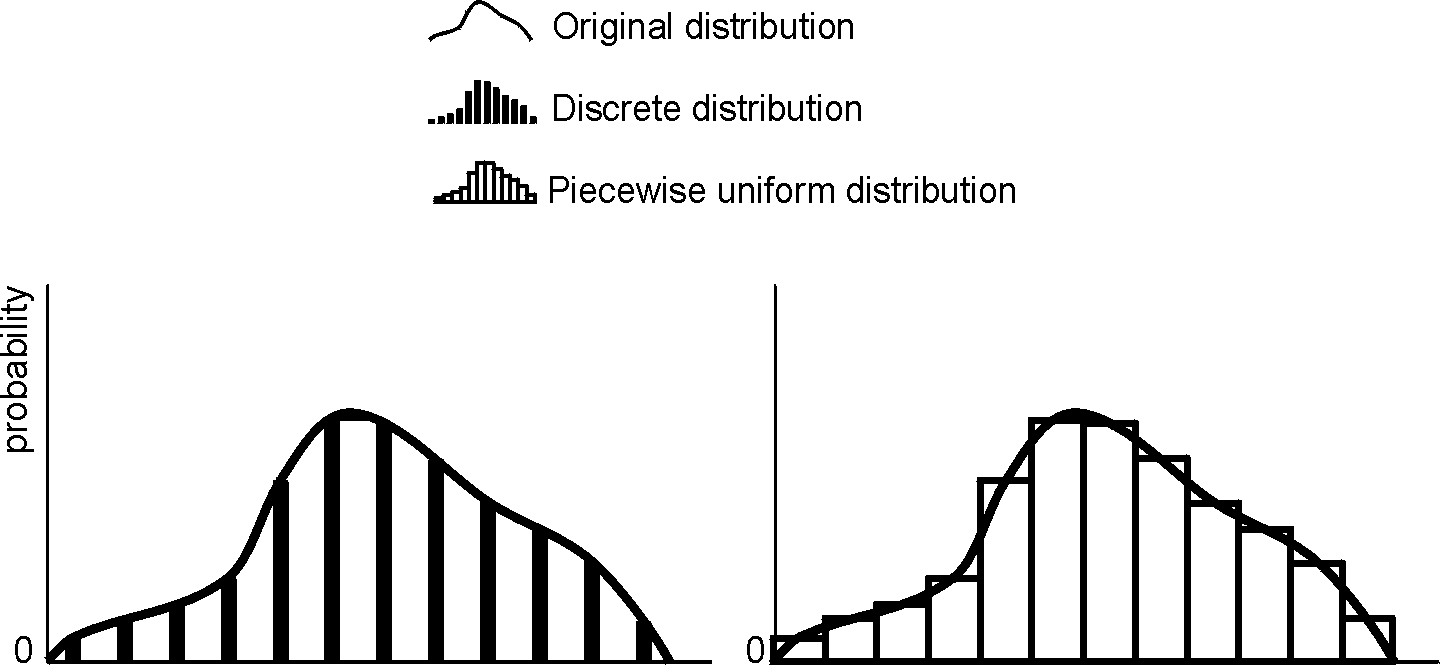
Fig. 2: Discrete and continuous distribution

Since the range of the most random variables is limited to the interval [a, b] a histogram defined on the limited interval can be used for the approximation. General discrete and piecewise uniform distributions defined on the limited interval can be very efficiently generated using the modified inverse distribution function method with tabulated values of the quantile function [2], see Figure 3..

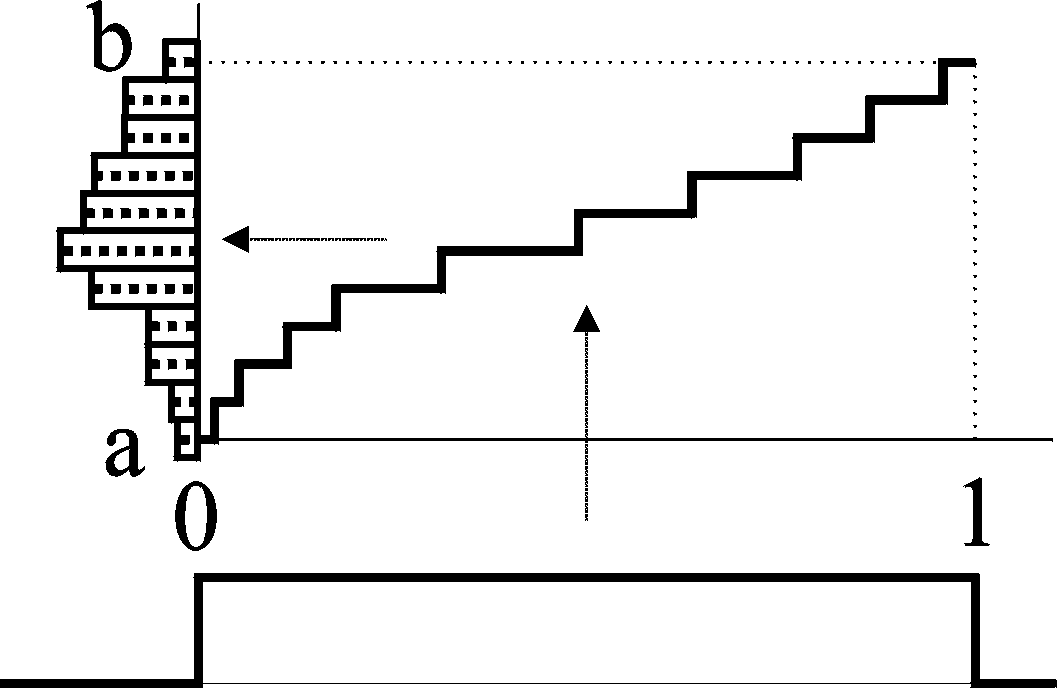
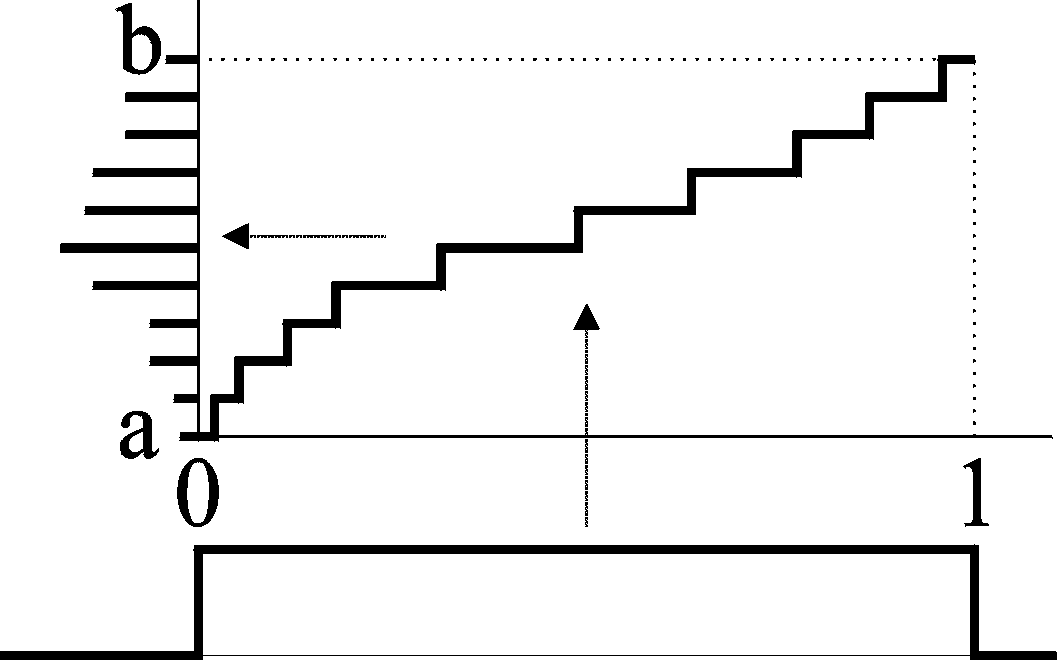
Fig. 3: Generation of piecewise uniform and general discrete distribution

References

[1] Silverman, B. W.: Density Estimation for Statistics and Data Analysis. Chapman and Hall, 1986.

[2] Marek, P.,Guštar, M.,Anagnos, T.: Simulation-Based Reliability Assessment for Structural Engineers. CRC Press, Boca Raton, Florida, 1995.