is
calculated by the following expression:Euro-SiBRAM’2002 Prague, June 24 to 26, 2002, Czech Republic
Session 5
Numerical Aspects of Simulation Based Reliability Assessment of Systems
Abstract
The purpose of this paper is to present a strategy for effective solving large simulation-based structural reliability problems. The presented approach is based on combination of the application of variance reduction techniques for reducing the numbers of simulation steps and the application of iterative solvers for reducing the cost of deterministic analysis. Our numerical experiments indicate efficiency of this strategy. Finally, advantages of using of intelligent information retrieval, parallel computing and Quasi-random numbers are discussed.
Key words: sampling techniques, simulation techniques, variance reduction, linear systems, iterative method, multiple right-hand sides, latent semantic indexing, dimensionality reduction, parallel computing, quasi-random numbers
Application of Monte Carlo method to Simulation Based Reliability Assessment concept (see SBRA [0] and [14]) involves repeated deterministic analysis of a problem. The purpose of our work is to accelerate reliability analysis of large systems by the two following approaches:
1. To reduce the number of Monte-Carlo steps by using "sophisticated" Monte-Carlo techniques.
2. To reduce the cost of deterministic analysis by exploiting the specific structure of our problem.
The structure of the paper is as follows. Section 2 reviews our experience with computer implementation of two well-known variance reduction techniques on to SBRA concept, namely Stratified Sampling and Importance Sampling. Our numerical experiments show that these sampling methods converge faster than usually used direct Monte-Carlo method. Sections 3 and 4 describes approaches for solving large multiple linear systems of equations by an iterative method which can be comprehended as an extension of popular conjugate gradients method [8], [10]. The effective solution of large multiple linear systems play key role, especially for simulation of large second-order problems. The presented algorithms accelerate the solution process by reusing information among linear equations. The extensive numerical experiments [5], [6], [7], [25] and theoretical results [2] indicates that presented algorithms solves real large problems faster than usually used solvers, where solutions are obtained independently. Finally, future advancements of reliability assessment, namely an application of intelligent information retrieval, effects of parallel computing and Quasi-random numbers are discussed in section 5.
The direct Monte-Carlo method is
very graphic tool for education purpose and the computer
implementation of this method is straightforward. On the other hand,
the direct Monte-Carlo method is not very suitable for effective
computer simulation of low occurrence rate events (failures), due to
the fact that the probability of failure
is
calculated by the following expression:
.
The symbol
denotes
the number of simulations where a failure occurred and the symbol
N denotes the total number of simulation steps.
In the reliability assessment, the probability of failure is the number which is usually very close to zero [14], [9], [1] and the large number of direct Monte-Carlo simulation steps have to be computed in this case due to the failure event rarity. This is very unwelcome fact, especially when each simulation step includes very time-consuming finite element analysis and processing [9].
It is well known fact, the efficiency of a simulation process can be improved by using variance reduction techniques (VRT) [1], [9], [16]. In this section we will discuss our experiences with implementation of variance reduction techniques onto SBRA concept.
Of course, the efficiency of a variance reduction technique can be significantly increased by involving additional information about structural behavior of a problem [1], [16]. On the other hand, our work is motivated by the requirement to use some variance reduction technique as a tool, which should be applied automatically in designer’s every-day work. For this reason, a variance reduction technique which will be used by designers should satisfied all at once the two following conditions:
1. A variance reduction technique must works correctly as a „blind“ tool as well in our case where it seems that no additional information about structural behavior of a simulated problem are usually available.
2. A variance reduction technique should over-perform direct Monte-Carlo method.
In the SBRA concept, the randomness of input variables is expressed by truncated histograms [14]. We implemented onto SBRA concept two kinds of VRT, namely Stratified Sampling and Importance Sampling. Algorithms were implemented in the Matlab system by Mathworks. The correctness of our computer implementations was successfully verified by comparing results taken from direct Monte-Carlo methods [0] and [14].
Our numerical experiments indicate that variance reduction techniques, which are based on Stratified Sampling and Importance Sampling, satisfy all at once conditions specified above.
The Stratified Sampling method consists of decomposition of range space D of random variable X into I disjoint subsets Di [1], [16].. The measure of i-th subset Di is determined by the expression
wi =P(XÎDi) ,
such that
holds.
Let the symbol Nif denotes the number of simulations in subset Di where a failure occurred and Ni is the total number of simulations in subset Di. Then the probability of failure pf is calculated by the following expression:
.
We can see, that direct Monte-Carlo method is a special case of Stratified Sampling method when no decomposition of range space D is implemented, that is when I = 1, i.e. D1 = D and w1 = 1.
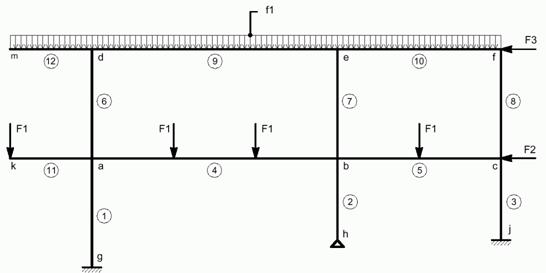
Fig. 1 Scheme of a planar statically indeterminate steel frame
Let us assume a planar statically indeterminate steel frame (see Fig. 1). We assumed random character of forces F1, F2 and F3. Randomness of these three random variables was expressed by histogram NORMAL3.HIS. We estimated probability of exceeding a critical value of deformation in a beam (for details see [19]). As a simulation tool we used Stratified Sampling method and for verification purpose direct Monte-Carlo method (see also [29]).
The efficiency of Stratified Sampling method depends on decomposition strategy of range space. We implemented following approach: Domains of all histograms were partitioned uniformly onto 7, 8 or 9 subsets. In all cases, the simulation process was computed without exploiting additional information about structural behavior, although our computer implementation allows exploiting of these informations.
To solve this problem using Stratified Sampling method, only 200 simulation steps were needed, whereas direct Monte-Carlo required more than five thousands of simulation steps to obtain the same results. In addition, the essence operation of Stratified Sampling, decomposition of range space, can be naturally used in SBRA concept because partitioning of truncated histograms is very effective to compute.
Failures will tend to occur when random parameters hold extreme values, usually in „tail“ regions [24]. Our numerical experiments verified that Stratified Sampling due to decomposition of range space allows to sample these active regions more effective than direct Monte-Carlo method even when the total number of simulation steps remain low.
The Importance Sampling method uses for sampling a new density function f*, which is called importance sampling density function. The purpose of this approach is to increase the frequency of occurrence of rare events (failures), even when the total number of simulation steps remain low, see [1], [16].
Let function
is
an indication of failure, i.e.
=
1 when a failure occurs, otherwise
=
0. The probability of failure is estimated by N
random samples X1* ;…;
XN* from X*, random variable with
density function f* by the expression
,
where
is
the ratio between initial and importance sampling density function.
Let us note that direct Monte-Carlo method is a special case of
Importance Sampling method when initial and importance sampling
density functions are the same so the measure
will
be unique equal to 1.
Determination of optimal f* claims additional information about structural behavior of a simulated problem. Authors in [1] uses so called Taguchi Design, for details see [26]. The integration of finite element method and Taguchi's approach is discussed in [15]. The question is whether this technique is applicable in designer‘s everyday work.
We implemented Importance Sampling method recently. In our implementation, we set f* as a uniform distribution. We solved a „tail“ problem – sum of two Binomial variables [14], pg. 71. When Importance Sampling method was applied, only 300 of simulation steps was enough to solve this problem, whereas direct Monte-Carlo required 50 000 of simulation steps to obtain the same results.
Our future work will be based on combination of Stratified Sampling and Importance Sampling [21].
Let us assume the following system of linear equations
K x = f ,
where K is a real
symmetric positive definite stiffness matrix of order n, in
which the vectors
and
contain,
respectively, the displacement and load vector.
There exist two basic approaches for solving of the linear systems of equation, namely direct and iterative methods.
The direct methods are widespread in commercial software thanks their robustness. Unfortunately, the algorithms of this type, such as Gaussian elimination, involve a factorization of stiffness matrix K. The factorization is memory and time consuming operation, which could become insufficient, especially for complex three-dimensional problems, where the matrix K is large. Furthermore, the factorized matrix contains usually more non-zero elements, so sparsity character of the stiffness matrix is broken.
On the other hand, the iterative methods generate a sequence of approximate solutions {xi}. These methods, such us popular conjugate gradient (CG) method [8], [10] involve the stiffness matrix K only in context of sparse matrix-vector multiplication, that keeps sparsity character of the method and a sophisticated storage system for sparse matrices can be used [27]. In addition, iterative solvers can be implemented very efficiently on massive parallel computers and their robustness can be increased by involving a preconditioning technique [4].
The CG algorithm starts from an
initial approximation
.
The i-th step consists the two following operations [10]:
1.
Construction of the new search direction vector
by
the form
,
where the coefficient
is
determined by the relation
and
the vector
is
called the residual vector.
2. Update of the new approximation
of the solution
where
.
The most expensive operation of the
CG algorithm is construction of the new search direction
vector
,
which involves computationally expensive the sparse matrix-vector
multiplication 
.
Usually, the iterative loop of CG
method is stopped when a norm of residual vector
is
smaller than a small positive real number, typically 1.10-4.
In this section, we will extend the CG method to effective solution of the linear system with the multiple right-hand sides (RHS).
Let us assume the following linear system of equations with q right-hand sides arisen from structural analysis with multiple load cases:
KX=F,
where K is a real
symmetric positive definite stiffness matrix of order n,
and
are
matrices,
in which
and
contain,
respectively, the displacement and load vector for i-th
condition.
There exists two basic approaches how to extend the CG method for effective solution of the linear system with the multiple right-hand sides, namely the Successive CG and the Block CG.
The idea of Successive CG is to
compute the most expensive operation of CG, the construction of the
new search direction vector
,
only for the one selected linear system of equation, called the seed
system. Solutions of the all unsolved linear systems are computed
using the search direction vector
from
the master RHS. When the master RHS is solved, SCG removes it from
the system and the other RHS is marked as a master. This strategy is
repeated until all the RHS are being solved.
The Successive CG is always stable. Theoretical results [2], [6] indicates that presented algorithm is efficient when RHS are close to each other.
The Block CG is a generalization of
the CG method. The new approximate solution
is
obtained by the form
,
where
is
the
matrix
of search directions and
is
the
step
length matrix. According to the generalization of CG,
.
Since the inversion matrix of
may
not exist, the Block CG is not stable, in general. On the other hand,
Block CG is powerful when the RHS are not close to each other.
To obtain the robust version
of Block CG, the direction matrix
must
preserve the full column rank. In our implementation [18], we
satisfied this condition by removing linearly dependent columns of
(Successive
Block CG). Then inversion of
will
be well defined and Successive Block CG will be stable.
Effectiveness of SBCG method is confirmed on solving a sensitivity
analysis of a tunnel, see Fig. 2. The shape of the tunnel is defined
by seven design variables on its curved edge. When semi-analytical
method is applied, the system of linear equations with eight RHS is
obtained. A direct solver required 7.810 Mbytes of memory to store
the factorized stiffness matrix. If a CG method is applied, the
amount of memory decreased to 1.018 Mbytes. Comparing repeated CG,
where the system is solved independently and SBCG algorithm, 226 %
acceleration was observed [18]. The problem was modeled on the system
ODESSY (Optimum DESign SYstem) developed on Institute of Mech. eng.
in Aalborg university, Denmark. Iterative algorithms were implemented
in the Matlab system and partially in ANSI C.
We have shortly described strategies for effective solution of the linear system with symmetric, positive definite stiffness matrix and with multiple right-hand sides. The ideas we have briefly mentioned here can be extended to systems, where the stiffness matrix is nonsymmetric [23]. Strategies for solving multiple linear systems with varying stiffness matrices and right-hand sides are studied in [3]. In all cases, the efficiency of iterative methods is achieved by sharing informations among linear systems.
In this section, let us shortly discussed future advancement of reliability assessment.
A simulation process creates lot of usually costly computed data, which contains informations about structure behavior of a simulated system. Several important properties of the simulated system, such as an estimation of the probability of a failure or the empiric density function can be quite easily picked up from the stored data. The question would be:
1. Is it possible to obtain from stored data the other interesting information?
2. How comprehensible visualize these picked up information to the user?
The quickly develop application of intelligent information retrieval is Latent Semantic Indexing [14]. Let us assume the following possible application of LSI: A designer asks a question, which includes a dangerous situation, which may occur in the simulated problem. The software will analyze the stored data taken from the simulation process and then returns to the user sets of parameters, which evoke the same or similar dangerous situations. The similarity is specified by the user defined similarity coefficient (a value between 0 and 1). Analyzing these sets of parameters, the designer can obtain the error sources.
We recently implemented the LSI procedure in Matlab. The LSI makes use of Singular value decomposition (SVD) of document matrix [8] which involves computationally expensive solution of partial eigen-value problem. The LSI procedure can be accelerated by an dimensionality reduction technique, for example by surprising simple random projection, where dimension of the problem is reduced by a random matrix whose columns have unit lengths [17].
The other interesting applications of data-mining and self-semantic organization of data is WEBSOM [28]. WEBSOM is a method for automatically organizing collections of text documents and for preparing visual maps of them to facilitate the mining and retrieval of information. Data taken from more than one million of Usenet newsgroup documents are automatically semantically organized and than displayed onto a mouse-sensitive picture, where related documents appear close to each other.
Lately, there is a trend to connect computers by a computer network to share memory, disc and processor power. There exist freely available software libraries such as PVM or MPI, which allows to programmers write computer codes for parallel computer [11], [22].
The communication among processes is available only by sending/receiving of messages, which contain data. It is well known fact that simulation techniques and iterative solvers can be very well speeded-up by multiprocessing. The programming of a parallel computer code is not straightforward and the foolproof sequential version of a computer code is recommended to have before writing the parallel version of a code. Experiences with parallel implementation of iterative solvers are discussed in [4], [20].
Finally, let us make reference to the application of number theory. The purpose why Monte-Carlo works is not random character of the method, but the uniformity. There exists sequences of deterministic values, for instance the Halton’s sequence or the Sobol’s sequence [16], which sample more uniformly than usually used sequences of independent random numbers even when the total number of samples remain low [12].
The paper presents a review of ideas, which would, hopefully, improve the Simulation Based Reliability Assessment concept of systems. I would like to thank to Professor Z. Dostál, Professor R. Briš and V. Vondrák (Dept. of Appl. Math., VŠB - Technical University of Ostrava, Czech Republic), Professor P. Marek (ITAM CAS, Prague, Czech Republic) and Professor A. Haldar (Dept. of Civil Engineering and Engineering Mechanics, University of Arizona, Tucson, USA) for their helpful comments of my work.
This work has been supported by the Council of Czech Government (CEZ MSM 2712400019).
References
[0] Marek P., Gustar M., and Anagnos, T. (1995). Simulation Based Reliability Assessment fir Structural Engineers. CRC Press Inc., Boca Raton, Florida.
[1] M. Beranger, B. Laurent: Quantification of rare accidental events on nuclear power plant, using Monte Carlo simulation. In ESREL 2001 European Safety & Reliability International Conference, Torino, Italy, pp. 871-878 (2001).
[2] T. F. Chan and W. L. Wan: Analysis of Projection Methods for Solving Linear Systems with Multiple Right-Hand Sides; ftp://ftp.math.ucla.edu/pub/camreport/cam94-26.ps.gz (1994).
[3] T. F. Chan and M. K. Ng, Galerkin Projection Methods for Solving Multiple Linear Systems, September; ftp://ftp.math.ucla.edu/pub/camreport/cam96-31.ps.gz (1996).
[4] Z. Dostál, D. Horák: Numerical and Parallel Scalability of FETI Algorithm for Variational Inequalities: Numerical Experiments; In Transactions of the VŠB - Technical University of Ostrava, Computer Science and Mathematics Series 1/2001, pp. 63 – 75 (2001).
[5] Z. Dostál, V. Vondrák and J. Rasmussen: Implementation of iterative solvers in shape optimization. In W. Gutkowski and Z. Mroz, editors, 2nd World Congress on Structural and Multidisciplinary Optimization, Zakopane, Poland, IFTR Warzsaw, pp. 443-448 (1997).
[6] C. Farhat, L. Crivelli, F. X. Roux: Extending substructure based iterative solvers to multiple load and repeated analyses, Comput. Methods Appl. Mech. Engrg, 117, pp. 195-209 (1994).
[7] Y.T. Feng, D. R. J. Owen, D. Peric: A block conjugate gradient method applied to linear system with multiple right hand sides. Comput. Methods in Appl. Mech. Eng., 127 (1995).
[8] G. H. Golub, C. F. Van Loan: Matrix Computations, The Johns Hopkins University Press (1989).
[9] A. Haldar, S. Mahahadevan: Reliability Assessment Using Stochastic Finite Element Analysis. Willey, New York (2000).
[10] M. R. Hestenes, E. Stiefel: Methods of Conjugate Gradients for Solving Linear Systems, J. Res. Nat. Bur. Stand. 49, 409-36 (1952).
[11] Internet Parallel Computing Archive; http://wotug.ukc.ac.uk/parallel/.
[12] C.Lemieux, P. L’Ecuyer: Using Lattice Rules for Variance Reduction in Simulation, Proceedings of the 2000 Winter Simulation Conference J. A. Joines, R. R. Barton, K. Kang, and P. A. Fishwick, eds; http://www.informs-cs.org/wsc00papers/070.PDF] (2000).
[13] LSI - Latent Semantic Indexing Web Site; http://www.cs.utk.edu/~lsi/.
[14] P. Marek, J., Brozzetti, M. Guštar: Probabilistic assessment of structures using Monte Carlo simulation: background, exercises and software, CRC Press, Inc., Boca Raton, Florida, U.S.A., (2001).
[15] S. Nellian: Integration of Taguchi design of experiments and finite element method for robust design http://www.ecs.umass.edu/mie/labs/mda/fea/sankar/layout.html.
[16] Numerical Recipes Books On-Line; http://www.nr.com/ .
[17] C. H. Papadimitriou, P. Raghavan, H. Tamaki, S. Vempala: Latent Semantic Indexing: A Probabilistic Analysis (1998); http://www-math.mit.edu/~vempala/papers/lsi.ps (1998).
[18] P. Praks: Conjugate gradient methods for linear systems with multiple right hand sides, In Transactions of the VŠB - Technical University of Ostrava, Computer Science and Mathematics Series 1/2001, pg. 129 - 138); http://praks.am.vsb.cz/research/praks.ps (2001).
[19] P. Praks., D. Pustka: Analysis of a Planar Statically Indeterminate Steel Frame Using Stratified Sampling Method (in Czech), to appear in Proceedings of Faculty of Civil Engineering, Technical University of Košice, Slovakia (2002).
[20] P. Praks: Iterative solution methods for solving linear systems with multiple right hand sides, MSc. thesis, VŠB - TU Ostrava (1999).
[21] P. Praks., Ph.D. Thesis, VŠB - Technical University of Ostrava, in preparation.
[22] Paralel Virtual Machine, http://www.epm.ornl.gov/pvm/pvm_home.html.
[23] V. Simoncini, E. Gallopoulos: An Iterative Method for Nonsymmetric Systems with Multiple Right-Hand Sides (1995); http:// www.csrd.uiuc.edu/report/1242.ps.gz].
[24] M. Stein: Large Sample Properties of Simulations Using Latin Hypercube Sampling, Technometrics, Vol. 29, No. 2, May 1987, pp. 143-151 (1987).
[25] M. Suarjana, K. H. Law: Successive conjugate gradient methods for structural analysis with multiple load cases, Int. J. Num. Methods Eng., 37, 4/1994 pp. 185-4 203 (1994).
[26] Taguchi's Approach to Quality Engineering; http://www.cnde.iastate.edu/staff/bforoura/HTML/taguchi.html
[27] V. Vondrák: Description of the K3 sparse matrix storage system; http://www.ime.auc.dk/research/design/odessy/Ods_index.htm
[28] WEBSOM - A novel SOM-based approach to free-text mining; http://websom.hut.fi/
[29] Pustka D. (2002). PhD. Thesis, VSB TU Ostrava, Department of Civil Engineering.